题目内容
【题目】如图，点C在⊙O的直径AB上，AB=6，AC=1．点P为⊙O上的任意一点，当∠OPC取最大值时，则△OCP的面积为 ．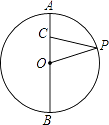 
【答案】
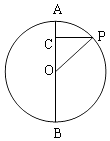
【解析】解：如图，当PC⊥AB时，∠OPC取最大值， ∵AB是⊙O的直径，AB=6，
∴OA=OP=3，
∵AC=1，
∴OC=2，
在Rt△OCP中，由勾股定理得：CP= 
= ，
∴S△OCP= 
OCPC= ×2× = ，
所以答案是： ．
【考点精析】掌握垂径定理和圆周角定理是解答本题的根本，需要知道垂径定理：平分弦（不是直径）的直径垂直于弦，并且平分弦所对的两条弧；顶点在圆心上的角叫做圆心角;顶点在圆周上，且它的两边分别与圆有另一个交点的角叫做圆周角;一条弧所对的圆周角等于它所对的圆心角的一半．
练习册系列答案
浙江名校名师金卷系列答案
相关题目
【题目】LED灯具有环保节能、投射范围大、无频闪、使用寿命较长等特点，在日常生活中，人们更倾向于LED灯的使用，某校数学兴趣小组为了解LED灯泡与普通白炽灯泡的销售情况，进行了市场调查：某商场购进一批30瓦的LED灯泡和普通白炽灯泡进行销售，其进价与标价如下表：
LED灯泡 | 普通白炽灯泡 | |
进价（元） | 45 | 25 |
标价（元） | 60 | 30 |
（1）该商场购进了LED灯泡与普通白炽灯泡共300个，LED灯泡按标价进行销售，而普通白炽灯泡打九折销售，当销售完这批灯泡后可以获利3200元，求该商场购进LED灯泡与普通白炽灯泡的数量分别为多少个？
（2）由于春节期间热销，很快将两种灯泡销售完，若该商场计划再次购进两种灯泡120个，在不打折的情况下，请问如何进货，销售完这批灯泡时获利最多且不超过进货价的30%，并求出此时这批灯泡的总利润为多少元？
