��Ŀ����
����Ŀ��С��ͬѧ��ѧ���ɶ���ʱ����һ�����������Σ���һ���������У����һ��������һ���ǵ�2������ô�����������Ϊ��������������.
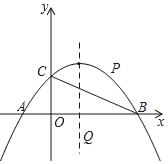
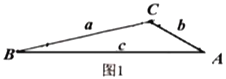
��ͼ1���ڱ���![]() �У�
��![]() ��
��![]() ��
��![]() ��
��![]() �ĶԱ߷ֱ��Ϊ
�ĶԱ߷ֱ��Ϊ![]() ��
��![]() ��
��![]() �����������
�����������![]() ��
��![]() ��
��![]() ��ʲô��ϵ�أ�������һ����̽������
��ʲô��ϵ�أ�������һ����̽������
��1����֪����������������һ���ڽ�Ϊ![]() ������������ε��������ǵĶ����ֱ�Ϊ______
������������ε��������ǵĶ����ֱ�Ϊ______
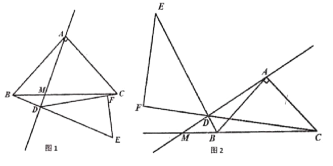
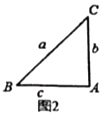
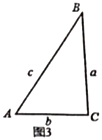
��2��С��ͬѧ�ȴ�������������������������о���������ͼ2��ͼ3��д�±���
������ | �ǵ���֪�� |
|
|
ͼ2 |
| ______ | ______ |
ͼ3 |
| ______ |
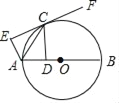
С��ͬѧ�����ϱ������һ���Բ��룺�����������������У�![]() ����ô
����ô![]() ��
��![]() ��
��![]() �������㣺______��
�������㣺______��
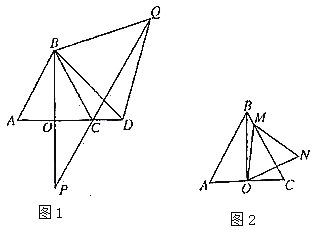
��3����ͼ1���ڱ����������У�![]() ��
��![]() ��
��![]() ��
��![]() �ĶԱ߷ֱ��Ϊ
�ĶԱ߷ֱ��Ϊ![]() ��
��![]() ��
��![]() ����֤��
����֤��![]() .
.
���𰸡���1��10�㣻20�㣻��2��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ����3��������.
����3��������.
��������
��1�����������ڽǺͣ����ɵý⣻
��2��ͼ2�������Σ���Ȼ�ǵ���ֱ�������Σ�����б��![]() Ϊ2����ô
Ϊ2����ô![]() ���������
���������![]() ��
��![]() ��ֵ��ͼ3�Ľⷨͬ�ϣ�
��ֵ��ͼ3�Ľⷨͬ�ϣ�
��3���ɣ�2���н��ۣ����μ��ɵ�֤.
��1�������⣬�����������ڽǺ�Ϊ180��-150��=30��
�ɱ��ǹ�ϵ�������������ڽǵĶ����ֱ�Ϊ10�㡢20�㣻
��2����б��Ϊ2��
��![]() ʱ����ô
ʱ����ô![]() ��
��
��![]()
��![]() ʱ��
ʱ��![]()
��![]()
![]() ��
��![]() ��
��![]() �������㣺
�������㣺![]() ��
��
��3���ɣ�2���н��ۣ���
![]()
��![]()
���ɵ�֤.