题目内容
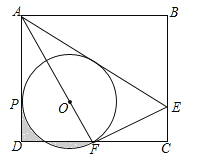
【题目】如图,在![]() 中,
中,![]() ,
,![]() .
.
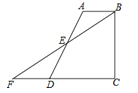
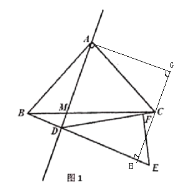
(1)如图1,若直线![]() 与
与![]() 相交于
相交于![]() ,过点
,过点![]() 作
作![]() 于
于![]() ,连接
,连接![]() 并延长
并延长![]() 至
至![]() ,使得
,使得![]() ,过点
,过点![]() 作
作![]() 于
于![]() ,证明:
,证明:![]() .
.
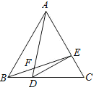
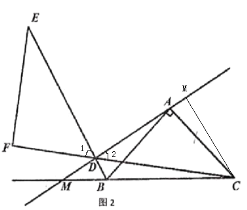
(2)如图2,若直线![]() 与
与![]() 的延长线相交于
的延长线相交于![]() ,过点
,过点![]() 作
作![]() 于
于![]() ,连接
,连接![]() 并延长
并延长![]() 至
至![]() ,使得
,使得![]() ,过点
,过点![]() 作
作![]() 交
交![]() 的延长线于
的延长线于![]() ,探究:
,探究:![]() 、
、![]() 、
、![]() 之间的数量关系,并证明.
之间的数量关系,并证明.
【答案】(1)见解析(2)AD+BD=EF,证明见解析
【解析】
(1)根据△ABC为等腰直角三角形,把△ABD逆时针旋转90°至△ACG,得到BD=GC,再延长GC交DE于H点,根据AD⊥BE可证四边形ADHG为正方形,得到AD=GH,再证明△DEF≌△DCH,得到EF=CH,则可证明![]() ;
;
(2)作CM⊥DA,先证明△DEF≌△CDM,得到EF=DM,再证明△ADB≌△CMA,得到BD=AM,根据AD+AM=DM=EF即可求解.
(1)如图,∵![]() ,
,![]() .
.
∴△ABC为等腰直角三角形,
把△ABD逆时针旋转90°至△ACG,
∴BD=CG,
延长GC交DE于H点,
∵AD⊥BE,∠DAG=90°=∠AGC,AD=AG,
∴四边形ADHG为正方形,
故∠DHC=90°,
∴AD=GH,
∵![]() ,
,![]() ,∠EDF=∠CDH
,∠EDF=∠CDH
∴△DEF≌△DCH,
∴EF=CH,
∴![]() ;
;
(2)AD+BD=EF,理由如下:
如图,作CM⊥DA,
∵AD⊥BE,
∴∠1+∠2=90°,
∵∠DCM+∠2=90°
∴∠1=∠DCM
∵∠F=∠DMC=90°,DE=DC
∴△DEF≌△CDM,
∴EF=DM,
∵![]() .
.
∴∠DAB+∠MAC=90°,
又∠DAB+∠DBA=90°
∴∠MAC=∠DBA
又AB=AC
∴△ADB≌△CMA,
∴BD=AM,
∴AD+BD=AD+AM=DM=EF
即AD+BD=EF,

 期末集结号系列答案
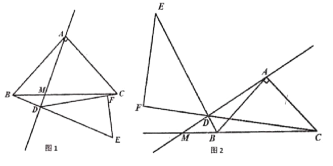
期末集结号系列答案【题目】小迪同学在学勾股定理时发现一类特殊三角形:在一个三角形中,如果一个角是另一个角的2倍,那么称这个三角形为“倍角三角形”.
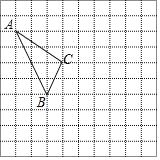
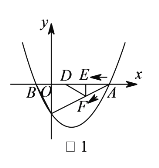
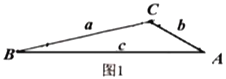
如图1,在倍角![]() 中,
中,![]() ,
,![]() 、
、![]() 、
、![]() 的对边分别记为
的对边分别记为![]() ,
,![]() ,
,![]() ,三角形的三边
,三角形的三边![]() ,
,![]() ,
,![]() 有什么关系呢?让我们一起来探索……
有什么关系呢?让我们一起来探索……
(1)已知“倍角三角形”的一个内角为![]() ,则这个三角形的另两个角的度数分别为______
,则这个三角形的另两个角的度数分别为______
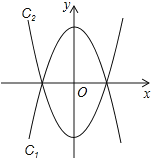
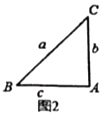
(2)小迪同学先从特殊的“倍角三角形”入手研究,请你结合图2和图3填写下表:
三角形 | 角的已知量 |
|
|
图2 |
| ______ | ______ |
图3 |
| ______ |
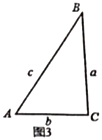
小迪同学根据上表,提出一般性猜想:在“倍角三角形”中,![]() ,那么
,那么![]() ,
,![]() ,
,![]() 三边满足:______;
三边满足:______;
(3)如图1:在倍角三角形中,![]() ,
,![]() 、
、![]() 、
、![]() 的对边分别记为
的对边分别记为![]() ,
,![]() ,
,![]() ,求证:
,求证:![]() .
.