题目内容
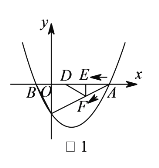
【题目】四个形状大小相同的等腰三角形按如图所示方式摆放，已知
，
，若点
落在
的延长线上，则图中阴影部分的面积为（ ）
A.
B.
C.
D.
【答案】A
【解析】
利用已知条件判定菱形，然后由四边形OHGK是平行四边形得OK=2，再由相似三角形，利用相似比求得OB，即可得其面积.
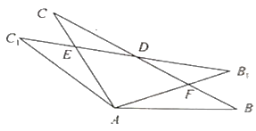
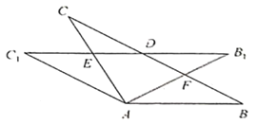
连接EF、GF，将△OHC沿点O顺时针旋转180°，如图所示：
由题意，得OB=OC=OA，∠EAO=∠AOF=∠FAO=∠AOE，GH⊥BO
∴AE∥FO，AF∥EO，GH∥OA
∴四边形AEOF为平行四边形
∴AE=EO
∴四边形AEOF为菱形
∴OH∥BF
∴四边形OHGK为平行四边形
∴OK=2
∵
∴△ABC为等腰三角形
∴∠GOF=90°，OG=OF
设四个相同的等腰三角形的腰长为
∵∠KOF=∠OBF，∠OFB=∠KFO
∴△OFB∽△KFO
∴
即
∴
∴阴影部分的面积为
故选：A.
练习册系列答案
相关题目
【题目】小迪同学在学勾股定理时发现一类特殊三角形：在一个三角形中，如果一个角是另一个角的2倍，那么称这个三角形为“倍角三角形”.
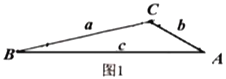
如图1，在倍角
中，
，
、
、
的对边分别记为
，
，
，三角形的三边，，有什么关系呢？让我们一起来探索……
（1）已知“倍角三角形”的一个内角为
，则这个三角形的另两个角的度数分别为______
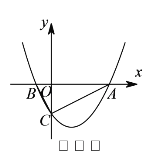
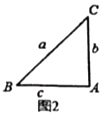
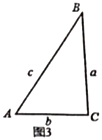
（2）小迪同学先从特殊的“倍角三角形”入手研究，请你结合图2和图3填写下表：
三角形 | 角的已知量 |
|
|
图2 |
| ______ | ______ |
图3 |
| ______ |
小迪同学根据上表，提出一般性猜想：在“倍角三角形”中，，那么，，三边满足：______；
（3）如图1：在倍角三角形中，
，、、的对边分别记为，，，求证：
.
