题目内容
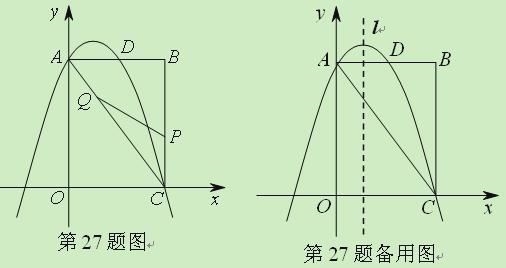
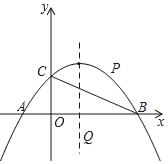
【题目】如图,已知点A(﹣1,0),B(3,0),C(0,1)在抛物线y=ax2+bx+c上.
(1)求抛物线解析式;
(2)在直线BC上方的抛物线上求一点P,使△PBC面积为1;
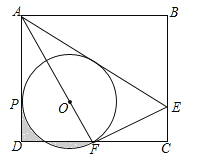
(3)在x轴下方且在抛物线对称轴上,是否存在一点Q,使∠BQC=∠BAC?若存在,求出Q点坐标;若不存在,说明理由.
【答案】(1)抛物线的解析式为y=﹣![]() x2+
x2+![]() x+1;(2)点P的坐标为(1,
x+1;(2)点P的坐标为(1,![]() )或(2,1);(3)存在,理由见解析.
)或(2,1);(3)存在,理由见解析.
【解析】
(1)设抛物线的解析式为y=a(x+1)(x﹣3),将C(0,1)代入求得a的值即可;
(2)过点P作PD⊥x,交BC与点D,先求得直线BC的解析式为y=﹣![]() x+1,设点P(x,﹣
x+1,设点P(x,﹣![]() x2+
x2+![]() x+1),则D(x,﹣
x+1),则D(x,﹣![]() x+1),然后可得到PD与x之间的关系式,接下来,依据△PBC的面积为1列方程求解即可;
x+1),然后可得到PD与x之间的关系式,接下来,依据△PBC的面积为1列方程求解即可;
(3)首先依据点A和点C的坐标可得到∠BQC=∠BAC=45°,设△ABC外接圆圆心为M,则∠CMB=90°,设⊙M的半径为x,则Rt△CMB中,依据勾股定理可求得⊙M的半径,然后依据外心的性质可得到点M为直线y=﹣x与x=1的交点,从而可求得点M的坐标,然后由点M的坐标以及⊙M的半径可得到点Q的坐标.
(1)设抛物线的解析式为y=a(x+1)(x﹣3),将C(0,1)代入得﹣3a=1,解得:a=﹣![]() ,
,
∴抛物线的解析式为y=﹣![]() x2+
x2+![]() x+1;
x+1;
(2)过点P作PD⊥x,交BC与点D,
设直线BC的解析式为y=kx+b,则![]() ,解得:k=﹣
,解得:k=﹣![]() ,
,
∴直线BC的解析式为y=﹣![]() x+1,
x+1,
设点P(x,﹣![]() x2+
x2+![]() x+1),则D(x,﹣
x+1),则D(x,﹣![]() x+1),
x+1),
∴PD=(﹣![]() x2+
x2+![]() x+1)﹣(﹣
x+1)﹣(﹣![]() x+1)=﹣
x+1)=﹣![]() x2+x,
x2+x,
∴S△PBC=![]() OBDP=
OBDP=![]() ×3×(﹣
×3×(﹣![]() x2+x)=﹣
x2+x)=﹣![]() x2+
x2+![]() x,
x,
又∵S△PBC=1,
∴﹣![]() x2+
x2+![]() x=1,整理得:x2﹣3x+2=0,解得:x=1或x=2,
x=1,整理得:x2﹣3x+2=0,解得:x=1或x=2,
∴点P的坐标为(1,![]() )或(2,1);
)或(2,1);
(3)存在.
∵A(﹣1,0),C(0,1),
∴OC=OA=1,
∴∠BAC=45°,
∵∠BQC=∠BAC=45°,
∴点Q为△ABC外接圆与抛物线对称轴在x轴下方的交点,
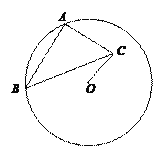
设△ABC外接圆圆心为M,则∠CMB=90°,
设⊙M的半径为x,则Rt△CMB中,由勾股定理可知CM2+BM2=BC2,即2x2=10,
解得:x=![]() (负值已舍去),
(负值已舍去),
∵AC的垂直平分线的为直线y=﹣x,AB的垂直平分线为直线x=1,
∴点M为直线y=﹣x与x=1的交点,即M(1,﹣1),
∴Q的坐标为(1,﹣1﹣![]() ).
).

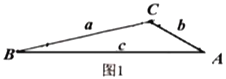
【题目】小迪同学在学勾股定理时发现一类特殊三角形:在一个三角形中,如果一个角是另一个角的2倍,那么称这个三角形为“倍角三角形”.
如图1,在倍角![]() 中,
中,![]() ,
,![]() 、
、![]() 、
、![]() 的对边分别记为
的对边分别记为![]() ,
,![]() ,
,![]() ,三角形的三边
,三角形的三边![]() ,
,![]() ,
,![]() 有什么关系呢?让我们一起来探索……
有什么关系呢?让我们一起来探索……
(1)已知“倍角三角形”的一个内角为![]() ,则这个三角形的另两个角的度数分别为______
,则这个三角形的另两个角的度数分别为______
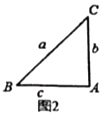
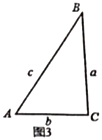
(2)小迪同学先从特殊的“倍角三角形”入手研究,请你结合图2和图3填写下表:
三角形 | 角的已知量 |
|
|
图2 |
| ______ | ______ |
图3 |
| ______ |
小迪同学根据上表,提出一般性猜想:在“倍角三角形”中,![]() ,那么
,那么![]() ,
,![]() ,
,![]() 三边满足:______;
三边满足:______;
(3)如图1:在倍角三角形中,![]() ,
,![]() 、
、![]() 、
、![]() 的对边分别记为
的对边分别记为![]() ,
,![]() ,
,![]() ,求证:
,求证:![]() .
.