题目内容
【题目】如图,在直角三角形ABC中,∠ACB=90°,将△ABC绕点C逆时针方向旋转,使点A落在AB边上的点D处,得到△DEC.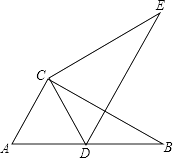
(1)点B的对应点是点 , BC的对应线段是 .
(2)判断△ACD的形状.
(3)若AD=CD,求∠B和∠BCE的度数.
【答案】
(1)E,EC
(2)解:△ACD是等腰三角形.
∵AC=CD,
∴△ACD是等腰三角形;
(3)解:∵AC=DC,AD=CD,
∴AD=DC=AD,
∴△ACD是等边三角形,
∴∠A=∠ACD=60°,
∵∠ACB=90°,
∴∴∠B=90°﹣60°=30°,
∴∠ACB=∠DCE,
∴∠BCE=∠ACD=60°.
【解析】解:(1)∵将△ABC绕点C逆时针方向旋转,使点A落在AB边上的点D处,得到△DEC.
∴点B的对应点是E,AC对应线段是EC.
(2)△ACD是等腰三角形.
∵AC=CD,
∴△ACD是等腰三角形;
(3)∵AC=DC,AD=CD,
∴AD=DC=AD,
∴△ACD是等边三角形,
∴∠A=∠ACD=60°,
∵∠ACB=90°,
∴∴∠B=90°﹣60°=30°,
∴∠ACB=∠DCE,
∴∠BCE=∠ACD=60°.
所以答案是:(1)E,EC;(2)等腰三角形;(3)60°.
【考点精析】根据题目的已知条件,利用旋转的性质的相关知识可以得到问题的答案,需要掌握①旋转后对应的线段长短不变,旋转角度大小不变;②旋转后对应的点到旋转到旋转中心的距离不变;③旋转后物体或图形不变,只是位置变了.

练习册系列答案
相关题目