题目内容
【题目】已知点P是半径为1的⊙O外一点，PA切⊙O于点A，且PA=1，AB是⊙O的弦，AB=
，连接PB，则PB= ．
【答案】1或
．
【解析】
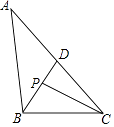
试题分析：连接OA，（1）如图1，连接OA，∵PA=AO=1，OA=OB，PA是⊙的切线，∴∠AOP=45°∵OA=OB，∴∠BOP=∠AOP=45°，在△POA与△POB中，∵OA=OB，∠AOP=∠BOP，OP=OP，∴△POA≌△POB，∴PB=PA=1；
（2）如图2，连接OA，与PB交于C，∵PA是⊙O的切线，∴OA⊥PA，而PA=AO=1，∴OP=
，∵AB=，而OA=OB=1，∴AO⊥BO，∴四边形PABO是平行四边形，∴PB，AO互相平分，设AO交PB与点C，即OC=
，∴BC=
，∴PB=．故答案为：1或．
练习册系列答案
相关题目
【题目】某中学为了让学生的跳远在中考体育测试中取得满意的成绩，在锻炼一个月后，学校对九年级一班的45名学生进行测试，成绩如下表：
跳远成绩（cm） | 160 | 170 | 180 | 190 | 200 | 220 |
人数 | 3 | 9 | 6 | 9 | 15 | 3 |
这些运动员跳远成绩的中位数和众数分别是（ ）
A.190，200
B.9，9
C.15，9
D.185，200
