题目内容
【题目】在等边三角形ABC中,点P在△ABC内,点Q在△ABC外,且∠ABP=∠ACQ,BP=CQ. 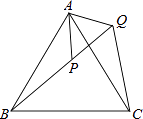
(1)求证:△ABP≌△CAQ;
(2)请判断△APQ是什么形状的三角形?试说明你的结论.
【答案】
(1)证明:∵△ABC为等边三角形,
∴AB=AC,∠BAC=60°,
在△ABP和△ACQ中,
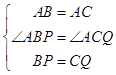 ,
,
∴△ABP≌△ACQ(SAS)
(2)解:∵△ABP≌△ACQ,
∴∠BAP=∠CAQ,AP=AQ,
∵∠BAP+∠CAP=60°,
∴∠PAQ=∠CAQ+∠CAP=60°,
∴△APQ是等边三角形
【解析】(1)根据等边三角形的性质可得AB=AC,再根据SAS证明△ABP≌△ACQ;(2)根据全等三角形的性质得到AP=AQ,再证∠PAQ=60°,从而得出△APQ是等边三角形.

练习册系列答案
相关题目