Question

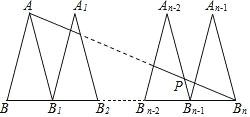
【题目】如图，△ABB1，△A1B1B2，…，△An﹣2Bn﹣2Bn﹣1，△An﹣1Bn﹣1Bn是n个全等的等腰三角形，其中AB=2，BB1=1，底边BB1，B1B2，…，Bn﹣2Bn﹣1，Bn﹣1Bn在同一条直线上，连接ABn交An﹣2Bn﹣1于点P，则PBn﹣1的值为__．

Answer 1

【答案】

【解析】

根据全等三角形的性质得到∠AB1B=∠PBn﹣1B，根据平行线的判定得到AB1∥PBn﹣1，根据相似三角形的性质即可得到结论．

解：∵△ABB1，△A1B1B2，…，△An﹣2Bn﹣2Bn﹣1，△An﹣1Bn﹣1Bn是n个全等的等腰三角形，

∴∠AB1B=∠PBn﹣1B，

∴AB1∥PBn﹣1，

∴PBnBn﹣1∽△ABnB1，

∴=．

∵AB1=AB=2，B1Bn=n﹣1，BnBn﹣1=1，

∴=，

∴PBn﹣1=．

故答案为：．