题目内容
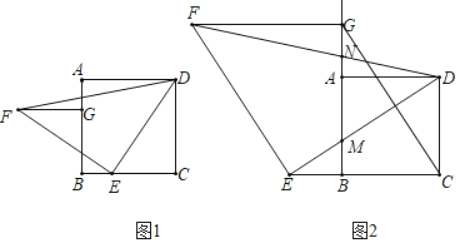
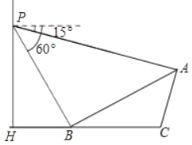
【题目】我们知道，如图1，AB是⊙O的弦，点F是
的中点，过点F作EF⊥AB于点E，易得点E是AB的中点，即AE＝EB．⊙O上一点C（AC＞BC），则折线ACB称为⊙O的一条“折弦”．
（1）当点C在弦AB的上方时（如图2），过点F作EF⊥AC于点E，求证：点E是“折弦ACB”的中点，即AE＝EC+CB．
（2）当点C在弦AB的下方时（如图3），其他条件不变，则上述结论是否仍然成立？若成立说明理由；若不成立，那么AE、EC、CB满足怎样的数量关系？直接写出，不必证明．
（3）如图4，已知Rt△ABC中，∠C＝90°，∠BAC＝30°，Rt△ABC的外接圆⊙O的半径为2，过⊙O上一点P作PH⊥AC于点H，交AB于点M，当∠PAB＝45°时，求AH的长．
【答案】（1）见解析；（2）结论AE＝EC+CB不成立，新结论为：CE＝BC+AE，见解析；（3）AH的长为
﹣1或+1．
【解析】
（1）在AC上截取AG＝BC，连接FA，FG，FB，FC，证明△FAG≌△FBC，根据全等三角形的性质得到FG＝FC，根据等腰三角形的性质得到EG＝EC，即可证明.
（2）在CA上截取CG＝CB，连接FA，FB，FC，证明△FCG≌△FCB，根据全等三角形的性质得到FG＝FB，得到FA＝FG，根据等腰三角形的性质得到AE＝GE，即可证明.
（3）分点P在弦AB上方和点P在弦AB下方两种情况进行讨论.
解：（1）如图2，
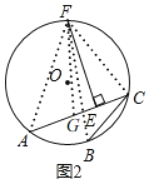
在AC上截取AG＝BC，连接FA，FG，FB，FC，
∵点F是
的中点，FA＝FB，
在△FAG和△FBC中，
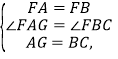
∴△FAG≌△FBC（SAS），
∴FG＝FC，
∵FE⊥AC，
∴EG＝EC，
∴AE＝AG+EG＝BC+CE；
（2）结论AE＝EC+CB不成立，新结论为：CE＝BC+AE，
理由：如图3，
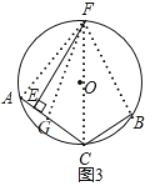
在CA上截取CG＝CB，连接FA，FB，FC，
∵点F是的中点，
∴FA＝FB，
,
∴∠FCG＝∠FCB，
在△FCG和△FCB中，
∴△FCG≌△FCB（SAS），
∴FG＝FB，
∴FA＝FG，
∵FE⊥AC，
∴AE＝GE，
∴CE＝CG+GE＝BC+AE；
（3）在Rt△ABC中，AB＝2OA＝4，∠BAC＝30°，
∴
当点P在弦AB上方时，如图4，
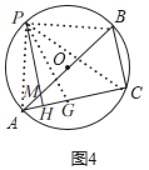
在CA上截取CG＝CB，连接PA，PB，PG，
∵∠ACB＝90°，
∴AB为⊙O的直径，
∴∠APB＝90°，
∵∠PAB＝45°，
∴∠PBA＝45°＝∠PAB，
∴PA＝PB，∠PCG＝∠PCB，
在△PCG和△PCB中，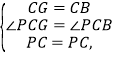 
∴△PCG≌△PCB（SAS），
∴PG＝PB，
∴PA＝PG，
∵PH⊥AC，
∴AH＝GH，
∴AC＝AH+GH+CG＝2AH+BC，
∴
∴
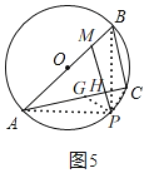
当点P在弦AB下方时，如图5，
在AC上截取AG＝BC，连接PA，PB，PC，PG
∵∠ACB＝90°，
∴AB为⊙O的直径，
∴∠APB＝90°，
∵∠PAB＝45°，
∴∠PBA＝45°＝∠PAB，
∴PA＝PB，
在△PAG和△PBC中，
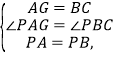
∴△PAG≌△PBC（SAS），
∴PG＝PC，
∵PH⊥AC，
∴CH＝GH，
∴AC＝AG+GH+CH＝BC+2CH，
∴
∴
∴
即：当∠PAB＝45°时，AH的长为
或
