题目内容
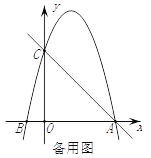
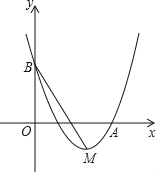
【题目】如图在平面直角坐标系xOy中，O为坐标原点，二次函数y=x2+bx+c的图象经过点A（3，0）、点B（0，3），顶点为M．
（1）求该二次函数的解析式；
（2）求∠OBM的正切值．
【答案】(1)y=x2﹣4x+3；（2）
【解析】分析：（1）先把A、B两点的坐标代入y=x2+bx+c得到关于b、c的方程组，然后解方程组求出b、c即可得到抛物线解析式；
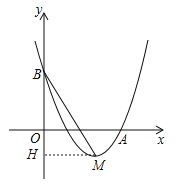
（2）作MH⊥y轴于H，如图，先把抛物线解析式配成顶点式得到M点坐标，然后根据正切的定义求∠HBM的正切值即可．
详解：（1）把A（3，0）、B（0，3）代入y=x2+bx+c得：
，
解得：
，所以y=x2﹣4x+3；
（2）作MH⊥y轴于H，如图，
∵y=x2﹣4x+3=（x﹣2）2﹣1，∴M（2，﹣1）．
∵MH⊥y轴，∴H（0，﹣1）．
在Rt△BMH中，tan∠HBM=
=，即∠OBM的正切值为．
练习册系列答案
一本好题口算题卡系列答案
相关题目
【题目】小方家住户型呈长方形，平面图如下(单位：米)，现准备铺设地面，三间卧室铺设木地板，其它区城铺设地砖.
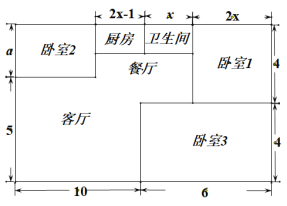
(1)求a的值.
(2)铺设地面需要木地板和地砖各多少平方米(用含
的代数式表示)？
(3)按市场价格，木地板单价为300元/平方米，地砖单价为100元/平方米，装修公司有
两种活动方案，如表：
活动方案 | 木地板价格 | 地砖价格 | 总安装费 |
A | 8折 | 8.5折 | 2000元 |
B | 9折 | 8.5折 | 免收 |
已知卧室2的面积是21平方米，则小方家应选择哪种活动，使铺设地面的总费用（包括材料费及安装费）更低？
