题目内容
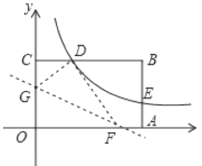
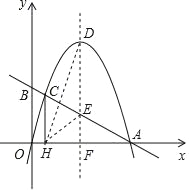
【题目】如图,二次函数y=﹣x2+bx的图象与x轴的正半轴交于点A(4,0),过A点的直线与y轴的正半轴交于点B,与二次函数的图象交于另一点C,过点C作CH⊥x轴,垂足为H.设二次函数图象的顶点为D,其对称轴与直线AB及x轴分别交于点E和点F.
(1)求这个二次函数的解析式;
(2)如果CE=3BC,求点B的坐标;
(3)如果△DHE是以DH为底边的等腰三角形,求点E的坐标.
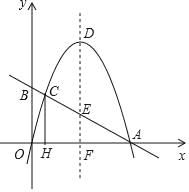
【答案】(1)y=﹣x2+4x;(2)B(0,2);(3)E(2,﹣12+8![]() )
)
【解析】整体分析:
(1)把A(4,0)代入抛物线y=﹣x2+bx即可求b;(2)由抛物线的性质求OF,AF的长,根据平行线分线段成比例定理,及CE=3BC,求OH,则可得CH,由△ACH∽△ABC求OB;(3)设点C的坐标为(x,﹣x2+4x),由△ACH∽△AEF,用x表示点E的坐标,根据ED=EH,用勾股定理列方程求解.
解:(1)∵抛物线y=﹣x2+bx经过点A(4,0),
∴﹣16+4b=0,∴b=4,
∴y=﹣x2+4x,
∴抛物线的解析式为y=﹣x2+4x;
(2)∵y=﹣(x﹣2)2+4,顶点D的坐标是(2,4),∴OF=AF=2,
∵BO∥CH∥EF,∴![]() =
=![]()
∵CE=3BC,∴![]() =
=![]() ,
,
∴OH=![]() ,∴CH=y﹣(
,∴CH=y﹣(![]() ﹣2)2+4=
﹣2)2+4=![]() ,
,
∵BO∥CH,∴△ACH∽△ABC,
∴![]() =
=![]() ,∴
,∴![]() =
=![]() ,∴OB=2,
,∴OB=2,
∴B(0,2);
(3)设点C的坐标为(x,﹣x2+4x),则H(x,0),
∵EF∥CH,∴△ACH∽△AEF,
∴![]() =
=![]() ,∴
,∴![]() =
=![]() ,∴EF=2x,∴E(2,2x),
,∴EF=2x,∴E(2,2x),
∵EH=DE,∴![]() =4﹣2x,
=4﹣2x,
∴x1=﹣6+4![]() ,x2=﹣6﹣4
,x2=﹣6﹣4![]() (舍),
(舍),
∴EF=2x=﹣12+8![]() ,
,
∴E(2,﹣12+8![]() ).
).

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目