题目内容
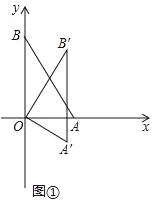
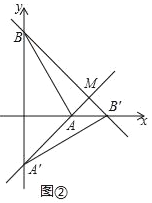
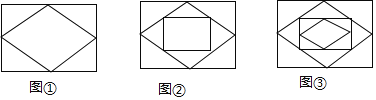
【题目】已知:顺次连接矩形各边的中点,得到一个菱形,如图①;再顺次连接菱形各边的中点,得到一个新的矩形.如图②;然后顺次连接新的矩形各边的中点,得到一个新的菱形,如图③;如此反复操作下去,则第3个图形中直角三角形的个数有______个,第2018个图形中直角三角形的个数有______个.
【答案】8; 4036
【解析】
写出前几个图形中的直角三角形的个数,并找出规律,当n为奇数时,三角形的个数是2(n+1),当n为偶数时,三角形的个数是2n,根据此规律求解即可.
解:第1个图形,有4个直角三角形,
第2个图形,有4个直角三角形,
第3个图形,有8个直角三角形,
第4个图形,有8个直角三角形,
…,
依此类推,当n为奇数时,三角形的个数是2(n+1),当n为偶数时,三角形的个数是2n个,
所以,第2018个图形中直角三角形的个数是2×2018=4036.
故答案是:8;4036.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
【题目】为了保护环境,某开发区综合治理指挥部决定购买A,B两种型号的污水处理设备共10台.已知用90万元购买A型号的污水处理设备的台数与用75万元购买B型号的污水处理设备的台数相同,每台设备价格及月处理污水量如下表所示:
污水处理设备 | A型 | B型 |
价格(万元/台) | m | m-3 |
月处理污水量(吨/台) | 220 | 180 |
(1)求m的值;
(2)由于受资金限制,指挥部用于购买污水处理设备的资金不超过165万元,问有多少种购买方案?并求出每月最多处理污水量的吨数.