题目内容
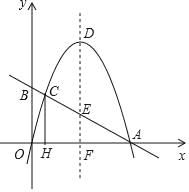
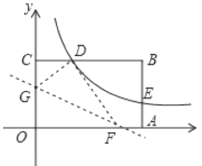
【题目】如图,矩形OABC的顶点A. C分别在x、y轴的正半轴上,点D为BC边上的点,反比例函数y=![]() (k≠0)在第一象限内的图象经过点D(m,2)和AB边上的点E(3,
(k≠0)在第一象限内的图象经过点D(m,2)和AB边上的点E(3,![]() ).
).
(1)求反比例函数的表达式和m的值;
(2)将矩形OABC的进行折叠,使点O于点D重合,折痕分别与x轴、y轴正半轴交于点F,G,求折痕FG所在直线的函数关系式。
【答案】(1)y=![]() ,m=1(2)y=
,m=1(2)y=![]() x+
x+![]()
【解析】
(1)由点E的坐标利用反比例函数图象上点的坐标特征即可求出k值,再由点B在反比例函数图象上,代入即可求出m值;
(2)设OG=x,利用勾股定理即可得出关于x的一元二次方程,解方程即可求出x值,从而得出点G的坐标.再过点F作FH⊥CB于点H,由此可得出△GCD∽△DHF,根据相似三角形的性质即可求出线段DF的长度,从而得出点F的坐标,结合点G、F的坐标利用待定系数法即可求出结论.
(1)∵反比例函数y=kx(k≠0)在第一象限内的图象经过点E(3, ![]() ),
),
∴k=3×![]() =2,
=2,
∴反比例函数的表达式为y=![]() .
.
又∵点D(m,2)在反比例函数y=![]() 的图象上,
的图象上,
∴2m=2,解得:m=1.
(2)设OG=x,则CG=OCOG=2x,
∵点D(1,2),
∴CD=1.
在Rt△CDG中,∠DCG=90°,CG=2x,CD=1,DG=OG=x,
∴CD![]() +CG
+CG![]() =DG
=DG![]() ,即1+(2x)
,即1+(2x)![]() =x
=x![]() ,
,
解得:x=![]() ,
,
∴点G(0, ![]() ).
).
过点F作FH⊥CB于点H,如图所示。
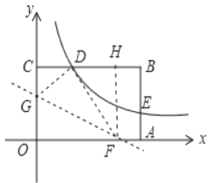
由折叠的特性可知:∠GDF=∠GOF=90°,OG=DG,OF=DF.
∵∠CGD+∠CDG=90°,∠CDG+∠HDF=90°,
∴∠CGD=∠HDF,
∵∠DCG=∠FHD=90°,
∴△GCD∽△DHF,
∴![]() ,
,
∴DF=2GD=![]() ,
,
∴点F的坐标为(![]() ,0).
,0).
设折痕FG所在直线的函数关系式为y=ax+,
∴有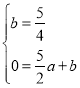 ,解得:
,解得: .
.
∴折痕FG所在直线的函数关系式为y=![]() x+
x+![]() .
.

【题目】某经销商从市场得知如下信息:
A品牌计算器 | B品牌计算器 | |
进价(元/台) | 700 | 100 |
售价(元/台) | 900 | 160 |
他计划用不超过4万元的资金一次性购进这两种品牌计算器共100台,设该经销商购进A品牌计算器x台,这两种品牌计算器全部销售完后获得利润为y元.
(1)求y与x之间的函数关系式;
(2)若要求全部销售完后获得的利润不少于1.26万元,该经销商有哪几种进货方案?
(3)选择哪种进货方案,该经销商可获利最大?最大利润是多少元?