题目内容
【题目】如图,在ABCD中,AB⊥AC,对角线AC,BD相交于点O,将直线AC绕点O顺时针旋转一个角度α(0°<α≤90°),分别交线段BC,AD于点E,F,连接BF.
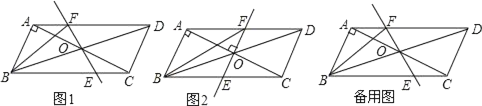
(1)如图1,在旋转的过程中,求证:OE=OF;
(2)如图2,当旋转至90°时,判断四边形ABEF的形状,并证明你的结论;
(3)若AB=1,BC=![]() ,且BF=DF,求旋转角度α的大小.
,且BF=DF,求旋转角度α的大小.
【答案】(1)证明见解析;(2)平行四边形,理由见解析;(3)45°
【解析】
(1)由平行四边形的性质得出∠OAF=∠OCE,OA=OC,进而判断出△AOF≌△COE,即可得出结论;
(2)先判断出∠BAC=∠AOF,得出AB∥EF,即可得出结论;
(3)先求出AC=2,进而得出A=1=AB,即可判断出△ABO是等腰直角三角形,进一步判断出△BFD是等腰三角形,利用等腰三角形的三线合一得出∠BOF=90°,即可得出结论.
(1)证明:在ABCD中,AD∥BC,
∴∠OAF=∠OCE,
∵OA=OC,∠AOF=∠COE,
∴△AOF≌△COE(ASA),
∴OE=OF;
(2)当旋转角为90°时,四边形ABEF是平行四边形,理由:
∵AB⊥AC,
∴∠BAC=90°,
∵∠AOF=90°,
∴∠BAC=∠AOF,
∴AB∥EF,
∵AF∥BE,
∴四边形ABEF是平行四边形;
(3)在Rt△ABC中,AB=1,BC=![]() ,
,
∴AC=![]() =2,
=2,
∴OA=1=AB,
∴△ABO是等腰直角三角形,
∴∠AOB=45°,
∵BF=DF,
∴△BFD是等腰三角形,
∵四边形ABCD是平行四边形,
∴OB=OD,
∴OF⊥BD(等腰三角形底边上的中线是底边上的高),
∴∠BOF=90°,
∴∠α=∠AOF=∠BOF﹣∠AOB=45°.

【题目】为了保护环境,某开发区综合治理指挥部决定购买A,B两种型号的污水处理设备共10台.已知用90万元购买A型号的污水处理设备的台数与用75万元购买B型号的污水处理设备的台数相同,每台设备价格及月处理污水量如下表所示:
污水处理设备 | A型 | B型 |
价格(万元/台) | m | m-3 |
月处理污水量(吨/台) | 220 | 180 |
(1)求m的值;
(2)由于受资金限制,指挥部用于购买污水处理设备的资金不超过165万元,问有多少种购买方案?并求出每月最多处理污水量的吨数.