题目内容
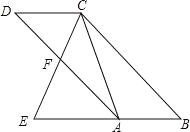
【题目】如图，在
中，AE
BC于点E，延长BC至点F，点使
，连接AF、DE、DF。
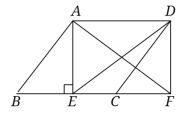
（1）求证：四边形AEFD是矩形；
（2）若
，
，，求AE的长。
【答案】（1）见解析 （2）
【解析】
（1）先证明四边形AEFD是平行四边形，再证明∠AEF=90°即可．
（2）证明△ABF是直角三角形，由三角形的面积即可得出AE的长．
解答：
(1)证明：∵CF=BE，
∴CF+EC=BE+EC.
即EF=BC.
∵在ABCD中,AD∥BC且AD=BC，
∴AD∥EF且AD=EF.
∴四边形AEFD是平行四边形。
∵AE⊥BC，
∴∠AEF=90.
∴四边形AEFD是矩形；
(2)∵四边形AEFD是矩形，DE=8，
∴AF=DE=8.
∵AB=6，BF=10，
∴
.
∴∠BAF=90°.
∵AE⊥BF，
∴△ABF的面积= 
ABAF= BFAE.
∴
.
【题目】某经销商从市场得知如下信息：
A品牌计算器 | B品牌计算器 | |
进价（元/台） | 700 | 100 |
售价（元/台） | 900 | 160 |
他计划用不超过4万元的资金一次性购进这两种品牌计算器共100台，设该经销商购进A品牌计算器x台，这两种品牌计算器全部销售完后获得利润为y元．
（1）求y与x之间的函数关系式；
（2）若要求全部销售完后获得的利润不少于1.26万元，该经销商有哪几种进货方案？
（3）选择哪种进货方案，该经销商可获利最大？最大利润是多少元？
【题目】为了保护环境，某开发区综合治理指挥部决定购买A，B两种型号的污水处理设备共10台．已知用90万元购买A型号的污水处理设备的台数与用75万元购买B型号的污水处理设备的台数相同，每台设备价格及月处理污水量如下表所示：
污水处理设备 | A型 | B型 |
价格（万元/台） | m | m-3 |
月处理污水量（吨/台） | 220 | 180 |
（1）求m的值；
（2）由于受资金限制，指挥部用于购买污水处理设备的资金不超过165万元，问有多少种购买方案？并求出每月最多处理污水量的吨数．