题目内容
已知在直角ABC中,∠C=900,AC=8㎝,BC=6㎝,则⊿ABC的外接圆半径长为_________㎝,⊿ABC的内切圆半径长为_________㎝,⊿ABC的外心与内心之间的距离为_________㎝。
5,2,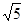
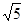
解:(1)∵∠C=90°,AC=8cm,BC=6cm,
∴AB=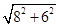 =10cm.
=10cm.
∴△ABC的外接圆半径长R=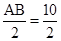 =5cm.
=5cm.
故答案为:5cm.
(2)∵AC=8cm,BC=6cm,由(1)知AB=10cm,
∴△ABC的内切圆半径长r=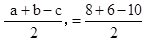
=2cm.
故答案为:2cm.
(3)连接ID,IE,IF,
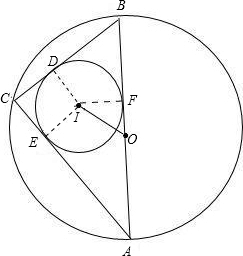
∵⊙I是△ABC的内切圆,
∴ID⊥BC,IE⊥AC,IF⊥AB,
∴∠CDI=∠CEI=∠C=90°,
又∵DI=EI,
∴四边形CDIE是正方形.
∴CD=CE=DI=IE,
由(2)知DI=IE=IF2cm,
∴CD=2cm.
∵BC=6cm,
∴BD=4cm.
∵⊙I是△ABC的内切圆,
∴BD=BF=4cm.
∵BO=5cm,
∴OF=1cm.
在Rt△IFO中,IO=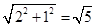 cm.
cm.
∴△ABC的外心与内心之间的距离为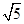 cm.
cm.
故答案为: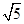 cm.
cm.
∴AB=
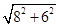 =10cm.
=10cm.∴△ABC的外接圆半径长R=
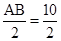 =5cm.
=5cm.故答案为:5cm.
(2)∵AC=8cm,BC=6cm,由(1)知AB=10cm,
∴△ABC的内切圆半径长r=
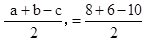
=2cm.
故答案为:2cm.
(3)连接ID,IE,IF,

∵⊙I是△ABC的内切圆,
∴ID⊥BC,IE⊥AC,IF⊥AB,
∴∠CDI=∠CEI=∠C=90°,
又∵DI=EI,
∴四边形CDIE是正方形.
∴CD=CE=DI=IE,
由(2)知DI=IE=IF2cm,
∴CD=2cm.
∵BC=6cm,
∴BD=4cm.
∵⊙I是△ABC的内切圆,
∴BD=BF=4cm.
∵BO=5cm,
∴OF=1cm.
在Rt△IFO中,IO=
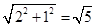 cm.
cm.∴△ABC的外心与内心之间的距离为
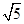 cm.
cm.故答案为:
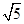 cm.
cm.
练习册系列答案
相关题目
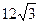 cm,∠OAB="30°."
cm,∠OAB="30°." 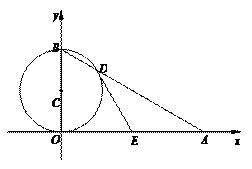
 B
B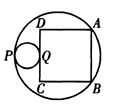
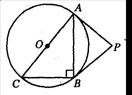
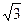 ,BC=1,求⊙O的半径.
,BC=1,求⊙O的半径. 是
是 的切线,
的切线, 为切点,
为切点, 是
是 ,则
,则 的度数是( )
的度数是( )




 的直径,CD为
的直径,CD为