题目内容
【题目】如图,已知抛物线y=x2﹣(m+3)x+9的顶点C在x轴正半轴上,一次函数y=x+3与抛物线交于A、B两点,与x、y轴分别交于D、E两点.
(1)求m的值;
(2)求A、B两点的坐标;
(3)当﹣3<x<1时,在抛物线上是否存在一点P,使得△PAB的面积是△ABC面积的2倍?若存在,请求出点P的坐标;若不存在,请说明理由.
【答案】
(1)
解:∵抛物线的顶点在x轴上,
∴它与x轴只有一个交点,
∴(m+3)2﹣4×9=0,
解得m=3或m=﹣9,
又∵抛物线对称轴大于0
∴﹣ ![]() >0,即m>﹣3,
>0,即m>﹣3,
∴m=3;
(2)
解:由(1)可得抛物的解析式为y=x2﹣6x+9,
解方程组 ![]() ,
,
得 ![]() 或
或 ![]() ,
,
∴点A的坐标为(1,4),点B的坐标为(6,9);
(3)
解:存在,
设点P(a,b),如图,作PT⊥x轴交BD于点E,AR⊥x轴,BS⊥x轴,
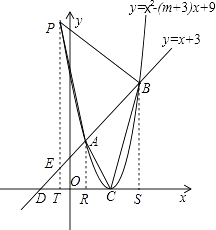
∵A(1,4),B(6,9),C(3,0),P(a,b)
∴AR=4,BS=9,RC=3﹣1=2,CS=6﹣3=3,RS=6﹣1=5,PT=b,RT=1﹣a,ST=6﹣a,
∴S△ABC=S梯形ARSB﹣S△ARC﹣S△BCS
= ![]() ×(4+9)×5﹣
×(4+9)×5﹣ ![]() ×2×4﹣
×2×4﹣ ![]() ×3×9
×3×9
=15,
S△PAB=S梯形PBST﹣S梯形ABSR﹣S梯形ARTP
= ![]() ×(9+b)(6﹣a)﹣
×(9+b)(6﹣a)﹣ ![]() ×(4+9)×5﹣
×(4+9)×5﹣ ![]() ×(b+4)(1﹣a)
×(b+4)(1﹣a)
= ![]() (5b﹣5a﹣15),
(5b﹣5a﹣15),
又∵S△PAB=2S△ABC,
∴ ![]() (5b﹣5a﹣15)=30,
(5b﹣5a﹣15)=30,
∴b﹣a=15,b=15+a,
∵点P在抛物线上
∴b=a2﹣6a+9,
∴15+a=a2﹣6a+9,
∴a2﹣7a﹣6=0,
解得:a= ![]() ,
,
∵﹣3<a<1,
∴a= ![]() ,
,
∴b=15+a= ![]() ,
,
∴P( ![]() ,
, ![]() ).
).
【解析】(1)由顶点在x轴上知它与x轴只有一个交点,即对应一元二次方程中△=0,可得关于m的方程,求解即可得m;(2)联立抛物线与直线解析式可得方程组,求解即可得A、B坐标;(3)设点P(a,b),作PT⊥x轴交BD于点E,AR⊥x轴,BS⊥x轴,分别表示出AR、BS、RC、CS、RS、PT、RT、ST的长,根据S△ABC=S梯形ARSB﹣S△ARC﹣S△BCS求出S△ABC , 由S△PAB=S梯形PBST﹣S梯形ABSR﹣S梯形ARTP表示出S△PAB , 根据△PAB的面积是△ABC面积的2倍可得a、b间关系,代入抛物线解析式即可求得.
【考点精析】掌握二次函数的图象是解答本题的根本,需要知道二次函数图像关键点:1、开口方向2、对称轴 3、顶点 4、与x轴交点 5、与y轴交点.

 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案