Question

【题目】如图，已知E是∠AOB的平分线上的一点，EC⊥OA，ED⊥OB，垂足分别是C，D．求证：OE垂直平分CD．

Answer 1

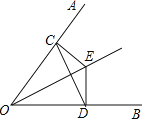
【答案】详见解析．

【解析】试题已知E是∠AOB的平分线上一点，EC⊥OB，ED⊥OA，根据角平分线的性质可得DE=CE，再由HL证得Rt△ODE≌Rt△OCE，可得出OD=OC，即可得△DOC是等腰三角形，由等腰三角形的性质即可得出OE是CD的垂直平分线．

试题解析：证明：∵E是∠AOB的平分线上一点，EC⊥OA，ED⊥OB，

∴DE=CE，OE=OE，

在Rt△ODE与Rt△OCE中，

，

∴Rt△ODE≌Rt△OCE（HL），

∴OD=OC，

∴△DOC是等腰三角形，

∵OE是∠AOB的平分线，

∴OE是CD的垂直平分线．