题目内容
【题目】如图,点A、B、C、D在同一条直线上,点E、F分别在直线AD的两侧,且AE=DF,∠A=∠D,AB=DC.
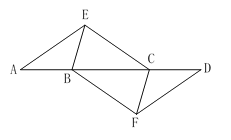
(1)求证:△ACE≌△DBF;
(2)求证:四边形BFCE是平行四边形.
【答案】证明见解析
【解析】试题分析:(1)根据已知条件易证AC=BD,再由SAS即可判定△ACE≌△DBF;(2)由△ACE≌△DBF,根据全等三角形的性质可得CE=BF,∠ACE=∠DBF, 即可得CE∥BF,所以四边形BFCE是平行四边形.
试题解析:
(1)∵AB=CD,
∴AB+BC=CD+BC,即AC=BD,
又∵AE=DF,∠A=∠D,
∴△ACE≌△DBF.
(2)∵△ACE≌△DBF,
∴CE=BF,∠ACE=∠DBF,
∴CE∥BF,
∴四边形BFCE是平行四边形.

练习册系列答案
 一线名师权威作业本系列答案
一线名师权威作业本系列答案
相关题目