��Ŀ����
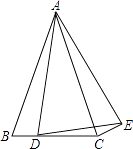
����Ŀ��ij��˾������һ���µĽ��ܲ�Ʒ���ò�Ʒ�ijɱ���Ϊ6Ԫ/�����ò�Ʒ����ʽͶ���г�ǰͨ�������������Ϊ��һ����(30��)�������ۣ��ۼ�Ϊ10Ԫ/����������Ա��������������˸��ټ�¼��������¼������Ƴ�ͼ��ͼ�е�����ABC��ʾ��������y(��)������ʱ��x(��)֮��ĺ�����ϵ��

(1)��y��x֮��ĺ�������ʽ����д��x��ȡֵ��Χ��
(2)���ý��ܲ�Ʒ������������ΪW(Ԫ)����W��x֮��ĺ�������ʽ�������������������1040Ԫ���������ж����죿
(3)��5��x��17��ֱ��д���ڼ�������������������������������Ƕ���Ԫ��
���𰸡���1��![]() ����2��������������1040Ԫ����������18������3����5�������������������������������880Ԫ.
����2��������������1040Ԫ����������18������3����5�������������������������������880Ԫ.
��������
��1������һ���ֶκ��������ô���ϵ������y��x֮��ĺ�������ʽ����ȷ��x��ȡֵ��Χ��
��2����������=���ۼ�-�ɱ��������������ɵ�w��x֮��ĺ�������ʽ�����ֱ���ݷֶκ�������������������1040Ԫ��Ӧ��x��ֵ��
��3���ֱ����5��x��10��10<x��17������Χ��������������Աȿɵý��ۣ�
��1�����߶�AB������ʾ�ĺ�����ϵʽΪy=ax+b��1��x��10����
BC�α�ʾ�ĺ�����ϵʽΪy=mx+n��10��x��30����
�ѣ�1,300������10,120������y=ax+b�е�![]() �����
�����![]() ��
��
���߶�AB��ʾ�ĺ�����ϵʽΪy=-20x+320��1��x��10����
�ѣ�10,120������30,400������y=mx+n�е�![]() �����
�����![]() ��
��
���߶�BC��ʾ�ĺ�����ϵʽΪy=14x-20��10��x��30����
��������![]() .
.
��2���������֪������Ʒ������Ϊ10-6=4(Ԫ/��)��
�൱1��x��10ʱ��w=4����-20x+320��=-80x+1280��
��10��x��30ʱ��w=4����14x-20��=56x-80��
��![]() ,������������1040Ԫ����w��1040��
,������������1040Ԫ����w��1040��
�൱1��x��10ʱ��w=-80x+1280��1040�����x��3��
��10��x��30ʱ��w=56x-80��1040�����x��20��
��3��x��20����������������1040Ԫ����������18��.
��3����5��x��17����5�������������������������������880Ԫ.