题目内容
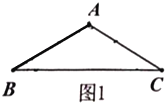
【题目】如图，
中，
，已知
，
与
相交于点
，
与相交于点
，
与相交于点
.
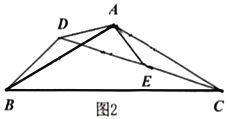
（1）如图，观察并猜想
和
有怎样的数量关系？并说明理由.
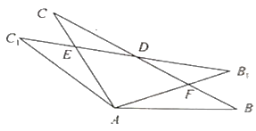
（2）筝形的定义：两组邻边分别相等的四边形叫做筝形. 如上图，证明四边形
是筝形.
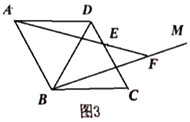
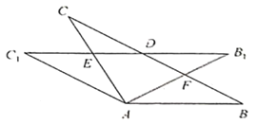
（3）如图，若
，其他条件不变，求
的长度.
【答案】（1）
，见解析；（2）见解析；（3）1
【解析】
（1）根据等边对等角的性质可得∠B=∠C，再根据旋转的性质可得∠BAF=∠C1AE，AB=AC=C1A=AB1，然后利用“角边角”证明△ABF和△C1AE全等，根据全等三角形对应边相等可得AE=AF，从而得解；
（2）先利用ASA证明
，得出
，再根据筝形的定义即可得证
（3）先根据
得出
，再根据含
角的直角三角形的性质得出
，再由
即可得出答案
（1）解：. 理由如下：
∵
中，
∴
∵
∴
，
，
∴
∴
在
和
中
∴
∴
∴
∴
（2）证明：由（1）可知
∴
，
又
∴
在
和
中
∴
∴
又∵
∴四边形
是筝形.
（3）解：∵
∴，
∴
在
中，
∴
∴
∴
答：
的长度为1.
练习册系列答案
名题金卷系列答案
优加精卷系列答案
相关题目
