题目内容
【题目】如图，已知△ABC的周长为20.
（1）尺规作图，画出线段AB的垂直平分线（不写作法，保留作图痕迹）；
（2）设AB的垂直平分线与BA交于点D，与BC交于点E，若AD＝4，求△ACE的周长.
【答案】(1)见解析;(2)12.
【解析】
（1）根据线段中垂线的尺规作图可得；
（2）根据垂直平分线的性质可得AB＝2AD＝8,AE＝BE,再根据三角形的周长定义即可求解.
解：（1）线段AB的垂直平分线如图所示
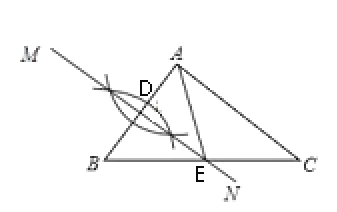
（2）∵DE是AB的垂直平分线，
∴AB＝2AD＝8，且AE＝BE,
∵△ABC的周长为AB＋BC＋CA＝20，
∴BC＋CA＝20－AB＝20－8＝12
∴△ACE的周长为AE＋EC＋CA＝BE＋EC＋CA＝BC＋CA＝12.
练习册系列答案
阳光课堂课时优化作业系列答案
相关题目
【题目】问题：探究函数y=|x|﹣2的图象与性质．
小华根据学习函数的经验，对函数y=|x|﹣2的图象与性质进行了探究．
下面是小华的探究过程，请补充完整：
（1）在函数y=|x|﹣2中，自变量x可以是任意实数；
（2）如表是y与x的几组对应值．
x | … | ﹣3 | ﹣2 | ﹣1 | 0 | 1 | 2 | 3 | … |
y | … | 1 | 0 | ﹣1 | ﹣2 | ﹣1 | 0 | m | … |
①m= ；
②若A（n，8），B（10，8）为该函数图象上不同的两点，则n= ；
（3）如图，在平面直角坐标系xOy中，描出以上表中各对对应值为坐标的点．并根据描出的点，画出该函数的图象；
根据函数图象可得：
①该函数的最小值为 ；
②已知直线
与函数y=|x|﹣2的图象交于C、D两点，当y1≥y时x的取值范围是 ．
