题目内容
【题目】在![]() 中,
中,![]() ,
,![]() ,
,![]() ,点
,点![]() 为射线
为射线![]() 上一点,当
上一点,当![]() 为等腰三角形时,
为等腰三角形时,![]() 的周长为 _______.
的周长为 _______.
【答案】32或![]() 或
或![]()
【解析】
分三种情况讨论:①如图1,当AB=AD=10时,CD=CB=6,得△ABD的周长为32m;
②如图2,当AB=BD=10时得CD=4,在Rt△ACD中,AD=![]() ,得到△ABD的周长=
,得到△ABD的周长=![]() ;
;
③如图3当AB为底时.则设腰AD=BD=x,则CD=x-6,在Rt△ACD中,由勾股定理得x2=(x-6)2+82,解得:x=![]() ,得到△ABD的周长为
,得到△ABD的周长为![]() m.
m.
解:在Rt△ABC中,AB=![]() ,
,
如图1,
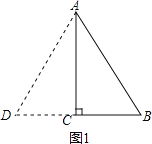
当AB=AD=10时,CD=CB=6,
得△ABD的周长为10+10+12=32m;
如图2,
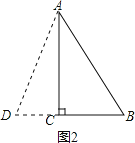
当AB=BD=10时,
得CD=4,
在Rt△ACD中,AD=![]()
∴△ABD的周长=10+10+![]() ;
;
如图3,

当AB为底时,设AD=BD=x,则CD=x-6,
在Rt△ACD中,AD2=CD2+AC2,
即x2=(x-6)2+82,解得:x=![]() ,
,
则△ABD的周长为![]() +
+![]() +10=
+10=![]() m.
m.
故答案为:32或![]() 或
或![]() .
.

【题目】如图1,点O是矩形ABCD的中心(对角线的交点),AB=4cm,AD=6cm.点M是边AB上的一动点,过点O作ON⊥OM,交BC于点N,设AM=x,ON=y,今天我们将根据学习函数的经验,研究函数值y随自变量x的变化而变化的规律.
下面是某同学做的一部分研究结果,请你一起参与解答:
(1)自变量x的取值范围是______;
(2)通过计算,得到了x与y的几组值,如下表:
x/cm | 0 | 0.5 | 1 | 1.5 | 2 | 2.5 | 3 | 3.5 | 4 |
y/cm | 2.40 | 2.24 | 2.11 | 2.03 | __ | __ | 2.11 | 2.24 | 2.40 |
请你补全表格(说明:补全表格时相关数值保留两位小数,参考数据:![]() ≈3.04,
≈3.04,![]() ≈6.09)
≈6.09)
(3)在如图2所示的平面直角坐标系中,画出该函数的大致图象.
(4)根据图象,请写出该函数的一条性质.







