题目内容
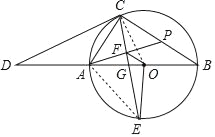
【题目】如图,AB为⊙O的直径,CD切⊙O于点C,与BA的延长线交于点D,OE⊥AB交⊙O于点E,连接CA、CE、CB,CE交AB于点G,过点A作AF⊥CE于点F,延长AF交BC于点P.
(Ⅰ)求∠CPA的度数;
(Ⅱ)连接OF,若AC=![]() ,∠D=30°,求线段OF的长.
,∠D=30°,求线段OF的长.

【答案】(Ⅰ)45°;(Ⅱ)![]()
【解析】
(Ⅰ)连接AE,由OA=OB且OE⊥AB知∠OEG+∠AEC=45°,再证∠OEG=∠BAP、∠AEC=∠ABP,在△ABP中利用三角形外角性质可得答案;
(Ⅱ)由切线性质及∠D=30°可得∠AOC=∠OAC=60°,在Rt△ABC中求得BC=3,由∠APC=45°、∠ACP=90°得CP=AC=![]() ,可知BP=3﹣
,可知BP=3﹣![]() ,证OF为△ABP中位线可得答案.
,证OF为△ABP中位线可得答案.
解:(Ⅰ)如图,连接AE,
∵OE⊥AB,OA=OE,
∴∠AOE=90°,∠AEO=45°,
∴∠OEG+∠OGE=90°,
∵AF⊥CE,
∴∠AFG=90°,
∴∠FAG+∠AGF=90°,
∵∠AGF=∠OGE,
∴∠OEG=∠BAP,
∵∠AEC=∠ABC,
∴∠APC=∠ABC+∠BAP=∠AEC+∠OEG=∠AEO=45°;
(Ⅱ)连接OC,
∵CD是⊙O的切线,
∴∠DCO=90°,
∵∠D=30°,
∴∠AOC=60°,
∵OA=OC,
∴∠BAC=60°,
在Rt△ABC中,AC=![]() ,
,
∴BC=ACtan∠BAC=![]() ×
×![]() =3,
=3,
由(1)知,AC=CP=![]() ,
,
∴BP=BC﹣CP=3﹣![]() ,
,
∵AF⊥CE,
∴AF=PF,
∵OA=OB,
∴OF=![]() BP=
BP=![]() .
.

 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案【题目】某校初三学生开展踢毽子比赛活动,每班派5名学生参加,按团体总分多少排列名次,在规定时间内每人踢100个以上(含100)为优秀.下表是成绩最好的甲班和乙班5名学生的比赛数据(单位:个):
1号 | 2号 | 3号 | 4号 | 5号 | 总数 | |
甲班 | 100 | 98 | 110 | 89 | 103 | 500 |
乙班 | 89 | 100 | 95 | 119 | 97 | 500 |
经统计发现两班总数相等.此时有学生建议,可以通过考察数据中的其他信息作为参考.
请你回答下列问题:
(1)填空:甲班的优秀率为 ,乙班的优秀率为 ;
(2)填空:甲班比赛数据的中位数为 ,乙班比赛数据的中位数为 ;
(3)填空:估计两班比赛数据的方差较小的是 班(填甲或乙)
(4)根据以上三条信息,你认为应该把冠军奖状发给哪一个班级?简述你的理由.