题目内容
【题目】综合与探究
问题情境:
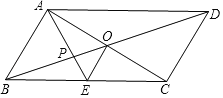
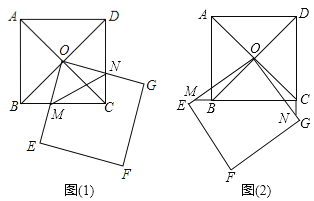
在综合实践课上,李老师让同学们根据如下问题情境,写出两个数学结论:如图(1),正方形ABCD的对角线交于点O,点O又是正方形OEFG的一个顶点(正方形OEFG的边长足够长),将正方形OEFG绕点O做旋转实验,OE与BC交于点M,OG与DC交于点N.
“兴趣小组”写出的两个数学结论是:
①S△OMC+S△ONC=![]() S正方形ABCD;
S正方形ABCD;
②BM2+CM2=2OM2.
问题解决:
(1)请你证明“兴趣小组”所写的两个结论的正确性.
类比探究:
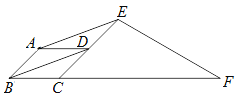
(2)解决完“兴趣小组”的两个问题后,老师让同学们继续探究,再提出新的问题;“智慧小组“提出的问题是:如图(2),将正方形OEFG在图(1)的基础上旋转一定的角度,当OE与CB的延长线交于点M,OG与DC的延长线交于点N,则“兴趣小组”所写的两个结论是否仍然成立?请说明理由.
【答案】(1)详见解析;(2)结论①不成立,结论②成立,理由详见解析.
【解析】
(1)①利用正方形的性质判断出△BOM≌△CON,利用面积和差即可得出结论;
②先得出OM=ON,BM=CN,再用勾股定理即可得出结论;
(2)同(1)的方法即可得出结论.
解:(1)①∵正方形ABCD的对角线相交于O,
∴S△BOC=![]() S正方形ABCD,OB=OC,∠BOC=90°,∠OBM=∠OCN,
S正方形ABCD,OB=OC,∠BOC=90°,∠OBM=∠OCN,
∵四边形OEFG是正方形,
∴∠MON=90°,
∴∠BOC﹣∠MOC=∠MON﹣∠MOC,
∴∠BOM=∠COM,
∴△BOM≌△CON,
∴S△BOM=S△CON,
∴S△OMC+S△ONC=S△OMC+S△BOM=![]() S正方形ABCD;
S正方形ABCD;
②由①知,△BOM≌△CON,
∴OM=ON,BM=CN,
在Rt△MCN中,MN2=CM2+CN2=CM2+BM2,
在Rt△MON中,MN2=OM2+ON2=2OM2,
∴BM2+CM2=2OM2;
(2)结论①不成立,
理由:∵正方形ABCD的对角线相交于O,
∴S△BOC=![]() S正方形ABCD,OB=
S正方形ABCD,OB=![]() BD,OC=
BD,OC=![]() AC,AC=BD,AC⊥BD,∠ABC=∠BCD=90°,AC平分∠BCD,BD平分∠ABC,
AC,AC=BD,AC⊥BD,∠ABC=∠BCD=90°,AC平分∠BCD,BD平分∠ABC,
∴OB=OC,∠BOC=90°,∠OBC=∠OCD=45°,
∴∠OBM=∠OCN=135°,
∵四边形OEFG是正方形,
∴∠MON=90°,
∴∠BOM=∠CON,
∴△BOM≌△CON,
∴S△BOM=S△CON,
∴S△OMC﹣S△BOM=S△OMC﹣S△CON=S△BOC=![]() S正方形ABCD,
S正方形ABCD,
∴结论①不成立;
结论②成立,理由:
如图(2)
连接MN,∵△BOM≌△CON,
∴OM=ON,BM=CN,
在Rt△MCN中,MN2=CM2+CN2=CM2+BM2,
在Rt△MON中,MN2=OM2+ON2=2OM2,
∴BM2+CM2=2OM2,
∴结论②成立.

 阅读快车系列答案
阅读快车系列答案