题目内容
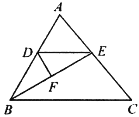
【题目】如图,平行四边形ABCD的对角线AC、BD相交于点O,AE平分∠BAD,分别交BC、BD于点E、P,连接OE,∠ADC=60°,AB=![]() BC=1,则下列结论:
BC=1,则下列结论:
①∠CAD=30°②BD=![]() ③S平行四边形ABCD=ABAC④OE=
③S平行四边形ABCD=ABAC④OE=![]() AD⑤S△APO=
AD⑤S△APO=![]() ,正确的个数是( )
,正确的个数是( )
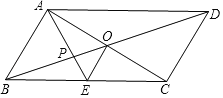
A. 2 B. 3 C. 4 D. 5
【答案】D
【解析】
①先根据角平分线和平行得:∠BAE=∠BEA,则AB=BE=1,由有一个角是60度的等腰三角形是等边三角形得:△ABE是等边三角形,由外角的性质和等腰三角形的性质得:∠ACE=30°,最后由平行线的性质可作判断;
②先根据三角形中位线定理得:OE=![]() AB=
AB=![]() ,OE∥AB,根据勾股定理计算OC=
,OE∥AB,根据勾股定理计算OC=![]() 和OD的长,可得BD的长;
和OD的长,可得BD的长;
③因为∠BAC=90°,根据平行四边形的面积公式可作判断;
④根据三角形中位线定理可作判断;
⑤根据同高三角形面积的比等于对应底边的比可得:S△AOE=S△EOC=![]() OEOC=
OEOC=![]() ,
,![]() ,代入可得结论.
,代入可得结论.
①∵AE平分∠BAD,
∴∠BAE=∠DAE,
∵四边形ABCD是平行四边形,
∴AD∥BC,∠ABC=∠ADC=60°,
∴∠DAE=∠BEA,
∴∠BAE=∠BEA,
∴AB=BE=1,
∴△ABE是等边三角形,
∴AE=BE=1,
∵BC=2,
∴EC=1,
∴AE=EC,
∴∠EAC=∠ACE,
∵∠AEB=∠EAC+∠ACE=60°,
∴∠ACE=30°,
∵AD∥BC,
∴∠CAD=∠ACE=30°,
故①正确;
②∵BE=EC,OA=OC,
∴OE=![]() AB=
AB=![]() ,OE∥AB,
,OE∥AB,
∴∠EOC=∠BAC=60°+30°=90°,
Rt△EOC中,OC=![]() ,
,
∵四边形ABCD是平行四边形,
∴∠BCD=∠BAD=120°,
∴∠ACB=30°,
∴∠ACD=90°,
Rt△OCD中,OD=![]() ,
,
∴BD=2OD=![]() ,故②正确;
,故②正确;
③由②知:∠BAC=90°,
∴SABCD=ABAC,
故③正确;
④由②知:OE是△ABC的中位线,
又AB=![]() BC,BC=AD,
BC,BC=AD,
∴OE=![]() AB=
AB=![]() AD,故④正确;
AD,故④正确;
⑤∵四边形ABCD是平行四边形,
∴OA=OC=![]() ,
,
∴S△AOE=S△EOC=![]() OEOC=
OEOC=![]() ×
×![]() ×
×![]() ,
,
∵OE∥AB,
∴![]() ,
,
∴![]() ,
,
∴S△AOP=![]() S△AOE=
S△AOE=![]() =
=![]() ,故⑤正确;
,故⑤正确;
本题正确的有:①②③④⑤,5个,
故选D.

【题目】体育课上,七年级某班男同学进行了100米测验,达标成绩为15秒,下表是梦想小组8名男生的成绩记录,其中“+”表示成绩大于15秒.
﹣0.8 | +1 | ﹣1.2 | 0 | ﹣0.7 | +0.6 | ﹣0.4 | ﹣0.1 |
问:(1)这个小组男生的达标率为多少?(达标率=![]() )
)
(2)这个小组男生的平均成绩是多少秒?