题目内容
【题目】某市居民使用自来水按月收费,标准如下:
①若每户月用水不超过![]() ,按
,按![]() 元/
元/![]() 收费;
收费;
②若超过![]() ,但不超过
,但不超过![]() ,则超过的部分按
,则超过的部分按![]() 元/
元/![]() 收费,未超过
收费,未超过![]() 部分按①标准收费;
部分按①标准收费;
③若超过![]() ,超过的部分按
,超过的部分按![]() 元/
元/![]() 收费,未超过
收费,未超过![]() 部分按②标准收费;
部分按②标准收费;
(1)若用水![]() ,应交水费______元;(用含
,应交水费______元;(用含![]() 的式子表示)
的式子表示)
(2)小明家上个月用水![]() ,交水费
,交水费![]() 元,求
元,求![]() 的值;
的值;
(3)在(2)的条件下,小明家七、八两个月共交水费![]() 元,七月份用水
元,七月份用水![]() 超过
超过![]() ,但不足
,但不足![]() ,八月份用水
,八月份用水![]() 超过
超过![]() ,当
,当![]() 均为整数时,求
均为整数时,求![]() 的值.
的值.
【答案】(1)25a;(2)a=3;(3)y=41或y=38.
【解析】
(1)根据题意的收费标准即可列出代数式;
(2)根据题意列出方程即可求出a的值;
(3)根据七月份用水![]() 超过
超过![]() ,但不足
,但不足![]() ,八月份用水
,八月份用水![]() 超过
超过![]() 列出二元一次方程,根据
列出二元一次方程,根据![]() 均为整数即可求解x,y的值.
均为整数即可求解x,y的值.
![]() 若用水
若用水![]() ,应交水费
,应交水费![]() ×(20-10)+10a=25a,
×(20-10)+10a=25a,
故答案为:25a;
![]() 根据题意,
根据题意,![]()
解得![]()
![]() 根据题意,
根据题意,![]() .
.
![]()
![]()
![]()
![]()
因为![]() 取
取![]() 至
至![]() 的整数,且
的整数,且![]() 为整数,所以
为整数,所以![]() 应为
应为![]() 的倍数.
的倍数.
当![]() 时,
时,![]() :
:
当![]() 时,
时,![]()

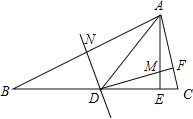
【题目】如图,△ABC中,∠ACB=90°,∠A=30°,AB=6,点P是斜边AB上一点(点P不与点A,B重合),过点P作PQ⊥AB于P,交边AC(或边CB)于点Q,设AP=x,△APQ的面积为y.
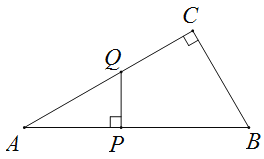
小明根据学习函数的经验,对函数y随自变量x的变换而变化的规律进行了探究.
下面是小明的探究过程,请补充完整:
(1)通过取点、画图、测量、计算,得到了x与y的几组值,如下表:
x | …… | 0.8 | 1.0 | 1.4 | 2.0 | 3.0 | 4.0 | 4.5 | 4.8 | 5.0 | 5.5 | …… |
y | …… | 0.2 | 0.3 | 0.6 | 1.2 | 2.6 | 4.6 | 5.8 | 5.0 | m | 2.4 | …… |
经测量、计算,m的值是 (保留一位小数).
(2)建立平面直角坐标系,描出以补全后的表中各对对应值为坐标的点,画出该函数的图象;

(3)结合几何图形和函数图象直接写出,当QP=CQ时,x的值是 .