题目内容
【题目】下列
个生产、生活现象中，可用“两点之间线段最短”来解释的是（ ）
A.用两根钉子就可以把木条固定在墙上
B.植树时，只要选出两棵树的位置，就能确定同一行树所在的直线
C.把弯曲的公路改直，就能缩短路程
D.砌墙时，经常在两个墙角的位置分别插一根木桩拉一条直的参照线
【答案】C
【解析】
逐一对选项进行分析即可．
A. 用两根钉子就可以把木条固定在墙上，用“两点确定一条直线”来解释，故错误；
B. 植树时，只要选出两棵树的位置，就能确定同一行树所在的直线，用“两点确定一条直线”来解释，故错误；
C. 把弯曲的公路改直，就能缩短路程，用“两点之间线段最短”来解释，故正确；
D. 砌墙时，经常在两个墙角的位置分别插一根木桩拉一条直的参照线，用“两点确定一条直线”来解释，故错误；
故选：C．
一线名师权威作业本系列答案
【题目】如图，△ABC中，∠ACB=90°，∠A=30°，AB=6，点P是斜边AB上一点（点P不与点A，B重合），过点P作PQ⊥AB于P，交边AC（或边CB）于点Q，设AP=x，△APQ的面积为y．
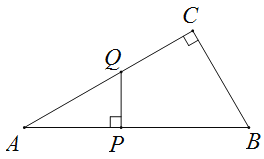
小明根据学习函数的经验，对函数y随自变量x的变换而变化的规律进行了探究．
下面是小明的探究过程，请补充完整：
（1）通过取点、画图、测量、计算，得到了x与y的几组值，如下表：
x | …… | 0.8 | 1.0 | 1.4 | 2.0 | 3.0 | 4.0 | 4.5 | 4.8 | 5.0 | 5.5 | …… |
y | …… | 0.2 | 0.3 | 0.6 | 1.2 | 2.6 | 4.6 | 5.8 | 5.0 | m | 2.4 | …… |
经测量、计算，m的值是 （保留一位小数）．
（2）建立平面直角坐标系，描出以补全后的表中各对对应值为坐标的点，画出该函数的图象；
（3）结合几何图形和函数图象直接写出，当QP=CQ时，x的值是 ．
【题目】某商场春节促销活动出售
两种商品，活动方案如下两种：
方案一 |
|
| |
每件标价 | 90元 | 100元 | |
每件商品返利 | 按标价的 | 按标价的 | |
例如买一件 | |||
方案二 | 所购商品一律按标价20％的返利 | ||
（1）某单位购买
商品
件，
商品20件，选用何种方案划算？
（2）某单位购买商品件（
为正整数），购买商品的件数是商品件数的2倍多1件。则两种方案的实际付款各多少？
（3）若两种方案的实际付款一样，求的值．