Question

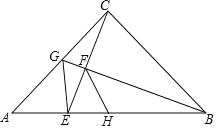
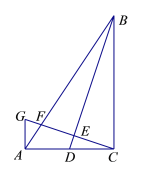
【题目】如图，在Rt△ABC中，∠ACB=90，AC=2，BC=3．点D为AC的中点，联结BD，过点C作CG⊥BD，交AC的垂线AG于点G，GC分别交BA、BD于点F、E．

（1）求GA的长；

（2）求△AFC的面积．

Answer 1

【答案】（1）；（2）.

【解析】

（1）由∠ACB=90，CG⊥BD，证得∠CBE =∠GCA，继而证得△BCD ∽△CAG，其对应边成比例求得答案；

（2）由GA∥BC，求得，根据等高的两个三角形面积的比等于底边的比即可求得答案.

（1）∵∠ACB=90°，

∴∠BCE+∠GCA=90°．

∵CG⊥BD，

∴∠CEB=90°，

∴∠CBE+∠BCE=90°，

∴∠CBE =∠GCA．

又∵∠DCB=∠GAC= 90°，

∴△BCD ∽△CAG．

∴，

∴，∴．

（2）∵∠GAC+∠BCA=180°，

∴GA∥BC．

∴．

∴．

∴．

∴．

又∵，

∴．