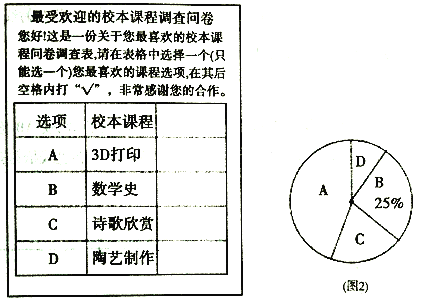
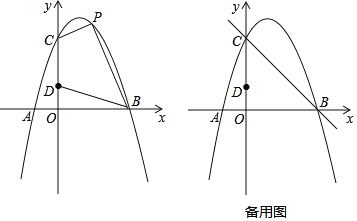
题目内容
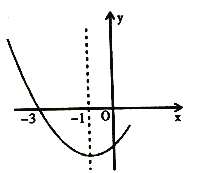
【题目】如图,已知二次函数![]() 的图象经过点
的图象经过点![]() .
.
(1)求![]() 的值和图象的顶点坐标;
的值和图象的顶点坐标;
(2)点![]() 在该二次函数图象上.
在该二次函数图象上.
①当![]() 时,求
时,求![]() 的值;
的值;
②若点![]() 到
到![]() 轴的距离小于2,请根据图象直接写出
轴的距离小于2,请根据图象直接写出![]() 的取值范围;
的取值范围;
③直接写出点![]() 与直线
与直线![]() 的距离小于
的距离小于![]() 时
时![]() 的取值范围.
的取值范围.
【答案】(1)![]() ,图象的顶点坐标为
,图象的顶点坐标为![]() ;(2)①当
;(2)①当![]() 时,
时,![]() ;②
;②![]() ;③
;③![]() .
.
【解析】
(1)根据待定系数法,即可求出a的值,把二次函数解析式,化为顶点式,即可得到顶点坐标;
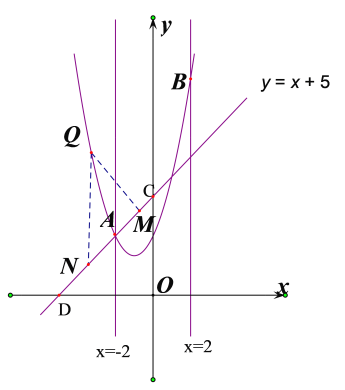
(2)①把![]() 代入二次函数解析式,即可;②设直线x=-2和直线x=2与抛物线的交点为A,B,可得:A(-2,3),B(2,11),进而即可求解;③设直线
代入二次函数解析式,即可;②设直线x=-2和直线x=2与抛物线的交点为A,B,可得:A(-2,3),B(2,11),进而即可求解;③设直线![]() 交x轴,y轴于点D,C,过点Q作QM⊥CD于点M,过点Q作QN∥y轴,交CD于点N,可得QNM是等腰直角三角形,当QM=
交x轴,y轴于点D,C,过点Q作QM⊥CD于点M,过点Q作QN∥y轴,交CD于点N,可得QNM是等腰直角三角形,当QM=![]() 时,则QN=2,设
时,则QN=2,设![]() ,N(m,m+5),列出关于m的方程,求出m的值,进而即可得到结论.
,N(m,m+5),列出关于m的方程,求出m的值,进而即可得到结论.
(1)把![]() 代入
代入![]() 中,得:
中,得:![]()
![]() ,
,
∴![]() ,
,
∴图象的顶点坐标为![]() ;
;
(2)①![]() 在该二次函数图象上,
在该二次函数图象上,
∴当![]() 时,
时,![]() ;
;
②设直线x=-2和直线x=2与抛物线的交点为A,B,如图,
把x=2或x=-2,代入![]() ,得y=11或3,
,得y=11或3,
∴A(-2,3),B(2,11),
当点![]() 到
到![]() 轴的距离小于2时,点Q在A,B之间的抛物线上(不包含A,B),
轴的距离小于2时,点Q在A,B之间的抛物线上(不包含A,B),
![]() ;
;
③设直线![]() 交x轴,y轴于点D,C,则D(-5,0),C(0,5),
交x轴,y轴于点D,C,则D(-5,0),C(0,5),
∴OC=OD,∠DCO=45°,
过点Q作QM⊥CD于点M,过点Q作QN∥y轴,交CD于点N,
∴∠QNM=∠DCO=45°,
∴QNM是等腰直角三角形,当QM=![]() 时,则QN=2,
时,则QN=2,
![]() 在该二次函数图象上,点N在直线
在该二次函数图象上,点N在直线![]() 上,
上,
∴设![]() ,N(m,m+5),
,N(m,m+5),
∴![]() ,化简得:
,化简得:![]() 或
或![]() ,
,
解得:![]() ,
,
∴点![]() 与直线
与直线![]() 的距离小于
的距离小于![]() 时
时![]() 的取值范围为:
的取值范围为:![]() .
.

 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案【题目】如下表,从左边第一个格子开始向右数,在每个小格子中都填入一个整数,使得其中仼意三个相邻格子中所填整数之和都相等.
|
|
|
| 5 | 4 | …… |
(1)可求得![]() _____;
_____;![]() _____;
_____;![]() _____.
_____.
(2)第2019个格子中的数为______;
(3)前2020个格子中所填整数之和为______.
(4)前![]() 个格子中所填整数之和是否可能为2020?若能,求出
个格子中所填整数之和是否可能为2020?若能,求出![]() 的值,若不能,请说明理由.
的值,若不能,请说明理由.