题目内容
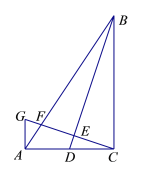
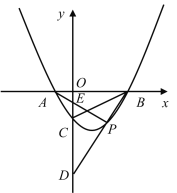
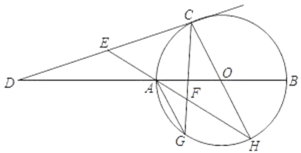
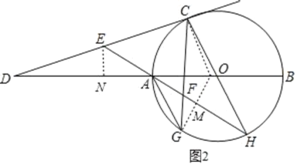
【题目】如图,已知AB为⊙O的直径,C为⊙O上异于A、B的一点,过C点的切线与BA的延长线交于D点,E为CD上一点,连接EA并延长交⊙O于H,F为EH上一点,且EF=CE,CF交延长线交⊙O于G.
(1)求证:弧AG=弧GH;
(2)若E为DC的中点,sim∠CDO=![]() ,AH=2
,AH=2![]() ,求⊙O的半径.
,求⊙O的半径.
【答案】(1)见解析;(2)⊙O的半径为3
【解析】
(1)连接AC,BC,根据AB为⊙O的直径,可得∠B+∠CAO=90°,根据CD为⊙O的切线,可得∠ECA+∠ACO=90°,再根据等边对等角和角的和差关系可得∠ACG=∠GAF=∠GCH,即可得证![]() .
.
(2)过点E作EN⊥DA,连接OC,OG,OG与AH交于点M,设CO=x,根据勾股定理、三角函数和相似三角形的性质列式求出x的值即可.
(1)证明:如图1,连接AC,BC,

∵AB为⊙O的直径,
∴∠ACB=90°,
∴∠B+∠CAO=90°,
∵CD为⊙O的切线,
∴∠ECA+∠ACO=90°,
∵OC=OA,
∴∠ACO=∠OAC,
∴∠ECA=∠B,
∵EF=CE,
∴∠ECF=∠EFC,
∵∠ECF=∠ECA+∠ACG,∠EFC=∠GAF+∠G,
∵∠ECA=∠B=∠G,
∴∠ACG=∠GAF=∠GCH,
∴![]() ;
;
(2)解:过点E作EN⊥DA,连接OC,OG,OG与AH交于点M,
∵![]() ,
,
∴OG⊥AH,AM=MH=![]() ,
,
∵CD是⊙O的切线,
∴∠DCO=90°,
设CO=x,
∵sin∠CDO=![]() =
=![]() ,
,
∴DO=3x,
∴![]() ,
,
∵E为DC的中点,
∴CE=DE=![]() =
=![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵∠EAN=∠OAM,∠ENA=∠OMA,
∴△AEN∽△AOM,
∴![]() ,
,
∴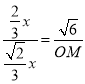 ,
,
∴OM=![]() ,
,
在Rt△AOM中,OA=![]() .
.
∴⊙O的半径为3.

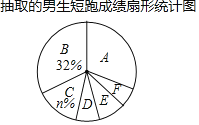
【题目】中国飞人苏炳添以6秒47获得2019年国际田联伯明翰室内赛男子60米冠军,苏炳添夺冠掀起跑步热潮某校为了解该校八年级男生的短跑水平,全校八年级男生中随机抽取了部分男生,对他们的短跑水平进行测试,并将测试成绩(满分10分)绘制成如下不完整的统计图表:
组别 | 成绩/分 | 人数/人 |
A | 5 | 36 |
B | 6 | 32 |
C | 7 | 15 |
D | 8 | 8 |
E | 9 | 5 |
F | 10 | m |
请你根据统计图表中的信息,解答下列问题:
(1)填空:m=_____,n=_____;
(2)所抽取的八年级男生短跑成绩的众数是_____分,扇形统计图中E组的扇形圆心角的度数为____°;
(3)求所抽取的八年级男生短跑的平均成绩.