题目内容
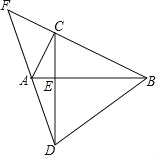
【题目】如图,△ABC中,∠ACB=90°,AC=BC,点G为AC中点,连结BG,CE⊥BG于F,交AB于E,连接GE,点H为AB中点,连接FH.以下结论:(1)∠ACE=∠ABG;(2)∠AGE=∠CGB:(3)若AB=10![]() ,则BF=4
,则BF=4![]() ;(4)FH平分∠BFE;(5)S△BGC=3S△CGE.其中正确结论的个数是( )
;(4)FH平分∠BFE;(5)S△BGC=3S△CGE.其中正确结论的个数是( )
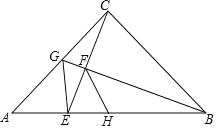
A.1B.2C.3D.4
【答案】D
【解析】
如图,作AP⊥AC交CE的延长线于P,连接CH.构造全等三角形,证明△CAP≌△BCG(ASA),△EAG≌△EAP(SAS),即可判断(2)(5)正确,利用相似三角形的判定与性质可以证明(4)正确,解直角三角形可以判定(3)正确.
如图,作AP⊥AC交CE的延长线于P,连接CH.

∵CE⊥BG,
∴∠CFB=∠ACB=90°.
∵∠ACE+∠BCE=90°,∠CBG+∠BCE=90°,
∴∠ACE=∠CBG.
∵BG是△ABC的中线,AB>BC,
∴BG不是∠ACB的角平分线,
∴∠ABG≠∠CBG,
∴∠ACE≠∠ABG,故(1)错误.
∵∠ACP=∠CBG,AC=BC,∠CAP=∠BCG=90°,
∴△CAP≌△BCG(ASA),
∴CG=PA=AG,∠BGC=∠P.
∵AG=AP,∠EAG=∠EAP=45°,AE=AE,
∴△EAG≌△EAP(SAS),
∴∠AGE=∠P,
∴∠AGE=∠CGB,故(2)正确.
∵AB=10![]() ,△ABC是等腰直角三角形,
,△ABC是等腰直角三角形,
∴AC=BC=10,
∴AG=CG=5,
∴BG![]()
![]() CGCB
CGCB![]() CF,
CF,
∴CF=2![]() ,
,
∴BF![]() ,故(3)正确.
,故(3)正确.
∵CA=CB,∠ACB=90°,AH=HB,
∴∠BCH=∠ACH=45°.
∵∠CFB=∠CHB=90°,∠COF=∠BOH,
∴△COF∽△BOH,
∴CO:OF=BO:OH.
∵∠COB=∠FOH,
∴△COB∽△FOH,
∴∠HFB=∠BCH=45°,
∴∠EFH=∠HFB=45°,
∴FH平分∠BFE,故(4)正确.
∵AG=GC,
∴S△CGE=S△AEG.
∵△AEG≌△AEP,
∴S△AEG=S△AEP,
∴S△GCE![]() S△ACP.
S△ACP.
∵△CAP≌△CBG,
∴S△ACP=S△CBG,
∴S△BGC=3S△CGE.故(5)正确.
故选D.

 红果子三级测试卷系列答案
红果子三级测试卷系列答案 课堂练加测系列答案
课堂练加测系列答案