题目内容
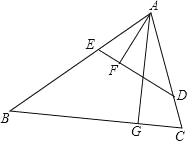
【题目】如图,以![]() 的
的![]() 边上一点
边上一点![]() 为圆心的圆,经过
为圆心的圆,经过![]() 、
、![]() 两点,且与
两点,且与![]() 边交于点
边交于点![]() ,
,![]() 为
为![]() 的下半圆弧的中点,连接
的下半圆弧的中点,连接![]() 交
交![]() 于
于![]() ,若
,若![]() .
.
(1)求证:![]() 是
是![]() 的切线;
的切线;
(2)若![]() ,
,![]() ,求
,求![]() 的半径.
的半径.

【答案】(1)见解析;(2)3
【解析】
(1)连接OA、OD,求出∠D+∠OFD=90°,推出∠CAF=∠CFA,∠OAD=∠D,求出∠OAD+∠CAF=90°,根据切线的判定推出即可;
(2)OD=r,OF=8-r,在Rt△DOF中根据勾股定理得出方程![]() ,求出即可.
,求出即可.
解:
(1)证明:连接OA,
∵D为BE的下半圆弧的中点,OD过圆心,
∴OD⊥BE,
∴∠ODF+∠OFD=90°,
∵CA=CF,
∴∠CAF=∠CFA,
而∠CFA=∠OFD,
∴∠ODF+∠CAF=90°,
∵OA=OD,
∴∠ODA=∠OAD,
∴∠OAD+∠CAF=90°,即∠OAC=90°,
∴OA⊥AC,OA是⊙O的半径,
∴AC是⊙O的切线;

(2)解:设⊙O的半径为r,则OF=4﹣r,
在Rt△ODF中,![]() ,解得r1=3,r2=1(舍去),
,解得r1=3,r2=1(舍去),
即⊙O的半径为3.

 应用题天天练四川大学出版社系列答案
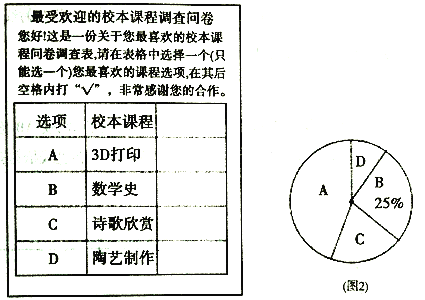
应用题天天练四川大学出版社系列答案【题目】为了解某区初二年级数学学科期末质量监控情况,进行了抽样调查,过程如下,请将有关问题补充完整.
收集数据:
随机抽取甲乙两所学校的 20 名学生的数学成绩进行
甲 | 91 | 89 | 77 | 86 | 71 | 31 | 97 | 93 | 72 | 91 |
81 | 92 | 85 | 85 | 95 | 88 | 88 | 90 | 44 | 91 | |
乙 | 84 | 93 | 66 | 69 | 76 | 87 | 77 | 82 | 85 | 88 |
90 | 88 | 67 | 88 | 91 | 96 | 68 | 97 | 59 | 88 |
整理、描述数据 :
按如下数据段整理、描述这两组数据
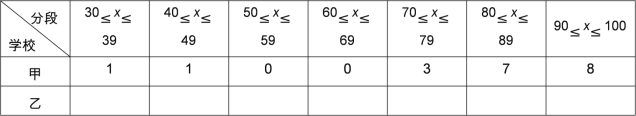
分析数据 :
两组数据的平均数、中位数、众数、方差如下表:

a经统计,表格中m的值是 ___________ .
得出结论:
b若甲学校有 400 名初二学生,估计这次考试成绩 80 分以上人数为____________ .
c可以推断出 _______学校学生的数学水平较高,理由为:①__________________;②_________________.(至少从两个不同的角度说明推断的合理性)
【题目】如下表,从左边第一个格子开始向右数,在每个小格子中都填入一个整数,使得其中仼意三个相邻格子中所填整数之和都相等.
|
|
|
| 5 | 4 | …… |
(1)可求得![]() _____;
_____;![]() _____;
_____;![]() _____.
_____.
(2)第2019个格子中的数为______;
(3)前2020个格子中所填整数之和为______.
(4)前![]() 个格子中所填整数之和是否可能为2020?若能,求出
个格子中所填整数之和是否可能为2020?若能,求出![]() 的值,若不能,请说明理由.
的值,若不能,请说明理由.