题目内容
【题目】如图,![]() 是
是![]() 的外接圆,
的外接圆,![]() 是
是![]() 的直径,点
的直径,点![]() 是半圆
是半圆![]() 的中点,点
的中点,点![]() 是
是![]() 上一动点(不与点
上一动点(不与点![]() 、
、![]() 重合),连接
重合),连接![]() 交
交![]() 于点
于点![]() .
.
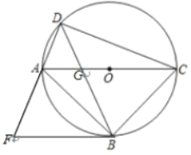
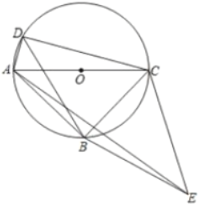
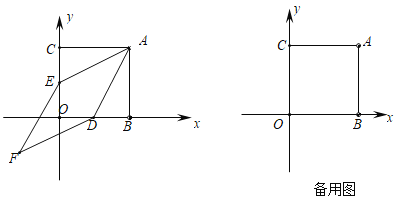
图1 图2
(1)如图1,过点![]() 作
作![]() ,交
,交![]() 延长线于点
延长线于点![]() ,求证:
,求证:![]() 与
与![]() 相切;
相切;
(2)若![]() ,
,![]() ,求
,求![]() 的长;
的长;
(3)如图2,把![]() 沿直线
沿直线![]() 翻折得到
翻折得到![]() ,连接
,连接![]() ,当点
,当点![]() 在
在![]() 运动时,探究线段
运动时,探究线段![]() 、
、![]() 、
、![]() 之间的数量关系,并说明理由.
之间的数量关系,并说明理由.
【答案】(1)详见解析;(2)![]() ;(3)
;(3)![]() ,详见解析.
,详见解析.
【解析】
(1)连接![]() ,求出
,求出![]() ,根据
,根据![]() 得到
得到![]() ,问题得证;
,问题得证;
(2)作![]() 交
交![]() 于点
于点![]() ,证明
,证明![]() ,求出CD=8,根据
,求出CD=8,根据![]() ,
,
在![]() 中,设
中,设![]() ,则
,则![]() ,
,![]() ,求出
,求出![]() ,
,![]() ,根据勾股定理即可求出CG;
,根据勾股定理即可求出CG;
(3)作![]() ,使得
,使得![]() ,连接
,连接![]() ,
,![]() .证明
.证明![]() ,得到
,得到![]() ,证明
,证明![]() ,得到
,得到![]() ,根据数量关系进行代换即可得到
,根据数量关系进行代换即可得到![]() .
.
证明:(1)连接![]() ,
,
![]() 是
是![]() 的外接圆,
的外接圆,![]() 是
是![]() 的直径,点
的直径,点![]() 是半圆
是半圆![]() 的中点,
的中点,
![]() ,
,![]()
![]()
![]()
![]()
![]()
![]() 与
与![]() 相切;
相切;
解:(2)作![]() 交
交![]() 于点
于点![]() ,
,
![]() 点
点![]() 是半圆周
是半圆周![]() 的中点,
的中点,
![]()
![]() 是
是![]() 的直径
的直径
![]()
![]()
![]()
在![]() 中,
中,![]() ,
,![]() ,
,
![]()
![]()
在![]() 中,设
中,设![]() ,则
,则![]() ,
,![]()
![]() ,
,![]() ,
,
在![]() 中,设
中,设![]() ,则
,则![]() ,
,![]()
∴,![]() ,
,![]()
在![]() 中,
中,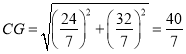
图1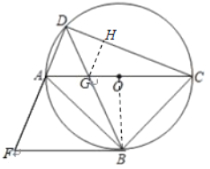
(3)结论:![]()
作![]() ,使得
,使得![]() ,连接
,连接![]() ,
,![]() .
.
![]() ,
,
![]() ,
,
![]() ,
,![]() ,
,
![]()
![]() ,
,
![]() ,
,
![]()
![]() ,
,
![]() ,
,
![]() ,
,![]() ,
,
![]()
图2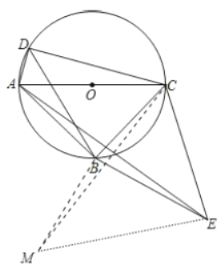

练习册系列答案
相关题目
【题目】甲、乙两家商场平时以同样价格出售相同的商品.春节期间两家商场都让利酬宾,其中甲商场所有商品按8折出售,乙商场对一次购物中不超过200元的不打折,超过200元后的价格部分打7折.
设商品原价为x元,顾客购物金额为y元.
(I).根据题意,填写下表:
商品原价 | 100 | 150 | 250 | … |
甲商场购物金额(元) | 80 | … | ||
乙商场购物金额(元) | 100 | … |
(Ⅱ).分别就两家商场的让利方式写出y关于x的函数关系式;
(Ⅲ).若x≥500时,选择哪家商场去购物更省钱?并说明理由.