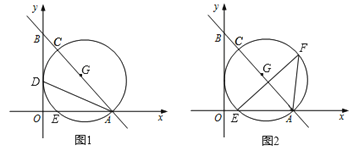题目内容
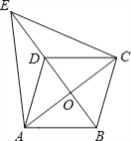
【题目】如图,![]() 中,
中,![]() 边上的高
边上的高![]() ,点
,点![]() 在
在![]() 上,且
上,且![]() ,点
,点![]() 在
在![]() 上,过点
上,过点![]() 作
作![]() 交
交![]() 于点
于点![]() ,当点
,当点![]() 在高
在高![]() 上移动时,点
上移动时,点![]() 可左右移动的最大距离是__________.
可左右移动的最大距离是__________.

【答案】4
【解析】
先求出AB及∠BAD=∠ABC=45°,当点F与点A重合时,DG=AD=3,即点G在点D右侧时最大值为3,过点E作EH⊥AD于H,设DG=y,DF=x,则FH=2-x,证明△EFH∽△FGD,得到![]() ,求出
,求出![]() ,当x=1时,y有最大值1,即点G在点D左侧时最大值为1,由此得到点G左右移动的距离.
,当x=1时,y有最大值1,即点G在点D左侧时最大值为1,由此得到点G左右移动的距离.
∵![]() ,
,
∴∠ADC=∠ADB=90°,
∵∠ABC=45°,
∴∠BAD=∠ABC=45°,
∴BD=AD=3,
∴CD=AB-BD=7-3=4,![]() ,
,
∵![]() ,
,
∴AE=![]() ,
,
当点F与点A重合时,如图1,
∵∠EFG=90°,
∴∠DAG=∠AGD=45°,
∴DG=AD=3,即点G在点D右侧时最大值为3,
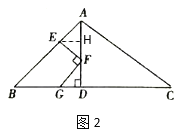
当点F向下移动到最低位置时,如图2,过点E作EH⊥AD于H,
∴AH=EH=1,∠EHF=90°,
∴DH=AD-AH=2,
设DG=y,DF=x,则FH=2-x,
∵∠EFG=90°,
∴∠EFH+∠GFD=90°,
∵∠HEF+∠EFH=90°,
∴∠HEF=∠GFD,
∵∠EHF=∠GDF=90°,
∴△EFH∽△FGD,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵-1<0,
∴当x=1时,y有最大值1,即点G在点D左侧时最大值为1,
∴点![]() 可左右移动的最大距离是3+1=4,
可左右移动的最大距离是3+1=4,
故答案为:4.

练习册系列答案
相关题目