题目内容
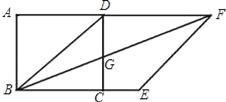
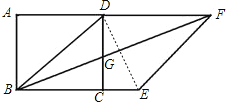
【题目】如图,正方形ABCD中,以对角线BD为边作菱形BDFE,使B,C,E三点在同一直线上,连接BF,交CD于点G.
(1)求证:CG=CE;
(2)若正方形边长为4,求菱形BDFE的面积.
【答案】(1)证明见解析;(2)16![]() .
.
【解析】
(1)连接DE,则DE⊥BF,可得∠CDE=∠CBG,根据BC=DC,∠BCG=∠DCE,可证△BCG≌△DCE,可证CG=CE;
(2)已知正方形的边长可以证明BD,即BE,根据BE,DC即可求菱形BDFE的面积.
解(1)证明:连接DE,则DE⊥BF,
∵∠CBG+∠BED=90°,∠CBG+∠CGB=90°,∠CGB=∠BED
又∵BC=DC,∠BCG=∠DCE,
∴△BCG≌△DCE(AAS),
∴CG=CE,
(2)正方形边长BC=4,则BD=BE=![]() ,DC=4,菱形BDFE的面积为S=4
,DC=4,菱形BDFE的面积为S=4![]() ×4=16
×4=16![]() .
.
答:菱形BDFE的面积为16![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目