题目内容
【题目】如图,在△ABC中,AB=AC,点D是△ABC内一点,AD=BD,且AD⊥BD,连接CD.过点C作CE⊥BC交AD的延长线于点 E,连接BE.过点D作DF⊥CD交BC于点F.
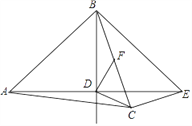
(1)若BD=DE=![]() ,CE=
,CE=![]() ,求BC的长;
,求BC的长;
(2)若BD=DE,求证:BF=CF.
【答案】(1)BC=2![]() ;(2)证明见解析.
;(2)证明见解析.
【解析】试题分析:(1)利用勾股定理求出BE的长,进而再次利用勾股定理求出BC的长;
(2)连接AF,首先利用ASA证明出△BDF≌△EDC,得到![]() ,进而得到∠ADF=∠BDC,再次利用SAS证出△ADF≌△BDC,结合题干条件得到AF⊥BC,利用等腰三角形的性质得到结论.
,进而得到∠ADF=∠BDC,再次利用SAS证出△ADF≌△BDC,结合题干条件得到AF⊥BC,利用等腰三角形的性质得到结论.
试题解析:(1)∵BD⊥AD,点E在AD的延长线上,
∴![]()
∵![]()
∴![]()
∵BC⊥CE,
∴![]()
∴![]()
(2)连接AF,

∵CD⊥BD,DF⊥CD,
∴![]()
∴∠BDF=∠CDE,
∵CE⊥BC,
∴![]()
∴∠DBC=∠CED,
在△BDF和△EDC中,
∵
∴△BDF≌△EDC(ASA),
∴DF=CD,
∴![]()
∵∠ADB=∠CDF,
∴∠ADB+∠BDF=∠CDF+∠BDF,
∴∠ADF=∠BDC,
在△ADF和△BDC中,
∵
∴△ADF≌△BDC(SAS),
∴∠AFD=∠BCD,
∴![]()
∴![]()
∴AF⊥BC,
∴AB=AC,
∴BF=CF.

练习册系列答案
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案
相关题目