题目内容
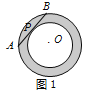
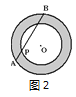
【题目】(1)如图1,同心圆中,大圆O的弦AB与小圆O切于点P,且AB=16,则圆环面积为________;
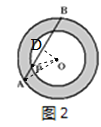
(2)如图2,同心圆中,大圆O的弦AB与小圆O相交,其中一个交点为点P,且AP=2,PB=8,则圆环面积为________.
【答案】 ![]()
![]()
【解析】分析:(1)根据圆环的面积等于两圆的面积差,再根据切线的性质定理、勾股定理、垂径定理求解;
(2)根据圆环的面积等于两圆的面积差,再根据垂径定理、勾股定理求解即可.
详解:(1)连接OA、OB、OP.
∵大圆的弦AB是小圆的切线,∴OP⊥AB,AP=PB,∴OB2﹣OP2=(16÷2)2=64.
∵S圆环=S大﹣S小=πOB2﹣πOP2=π(OB2﹣OP2),∴S圆环=64π.
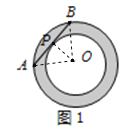
(2)过O作OD⊥AB于D,连接OP,OA.
∵AP=2,PB=8,∴AB=10.
∵OD⊥AB,∴AD=![]() AB=5.
AB=5.
∵AP=2,∴PD=3.
在Rt△AOD和Rt△POD中,
∵OA2=AD2+OD2,OP2=PD2+OD2,∴OA2-OP2= AD2-PD2= 52-32=16.
S圆环=S大﹣S小=πOA2﹣πOP2=π(OA2﹣OP2),∴S圆环=16π.
故答案为:(1)64π;(2)16π.

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目