题目内容
【题目】如图1,直线l : ![]() 经过定点P,交x、y轴于A、B两点.
经过定点P,交x、y轴于A、B两点.
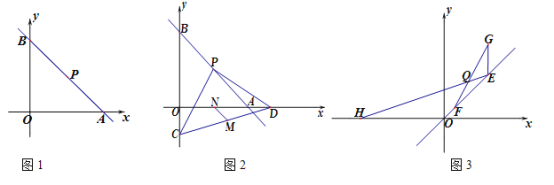
(1)如图1,直接写出点P的坐标__________________;
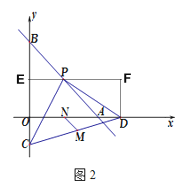
(2)如图2,当k=—1时,点C为y轴负半轴上一动点,过点P作PD⊥PC交x轴于点D,M、N分别为CD、OA的中点,求![]() 的值;
的值;
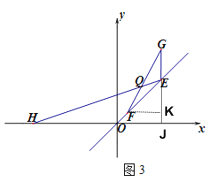
(3)如图3,E、F两点在射线OP上移动,EF=![]() ,点E向上移动2个单位得到点G,点E横坐标为 t(t>0),在x轴负半轴上有点H(—2t,0),FG与HE相交于Q点,求证:点Q在某条直线上运动,并求此直线的解析式.
,点E向上移动2个单位得到点G,点E横坐标为 t(t>0),在x轴负半轴上有点H(—2t,0),FG与HE相交于Q点,求证:点Q在某条直线上运动,并求此直线的解析式.
【答案】(1)(2,2);(2)![]() ;(3)点Q在直线
;(3)点Q在直线![]() 上运动.
上运动.
【解析】
(1)将直线l解析式变形可得到定点坐标;
(2)过点P作EF∥x轴,过点D作DF⊥EF垂足为F,首先证明△EPC≌△FDP,设C(0,m),则PF=CE=2-m,易得D(4-m,0),然后根据k=-1求出A点坐标,可得AD=-m,利用中点坐标公式和两点间距离公式求出MN,问题得解;
(3)如图3,延长GE交x轴于点J,则GJ⊥x轴,过点F作FK⊥GJ于点K,由OP所以直线解析式为y=x,可求得F点、G点坐标,然后用待定系数法求出直线HE和直线FG解析式,求出交点Q的坐标,即可解得点Q在直线![]() 上运动.
上运动.
解:(1)∵![]() ,
,
∴当x=2时,y=2,
∴定点P的坐标是(2,2);
(2)如图2,过点P作EF∥x轴,过点D作DF⊥EF垂足为F,
∵P(2,2),∴PE=OE=DF=2,
∵PD⊥PC,
∴∠EPC+∠FPD=90°,
∵∠EPC+∠ECP=90°,
∴∠FPD=∠ECP,
在△EPC和△FDP中,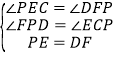 ,
,
∴△EPC≌△FDP(AAS),
∴PF=CE,
设C(0,m),则PF=CE=2-m,
∴OD=PE+PF=4-m,
∴D(4-m,0),
当k=-1时,直线l解析式为:![]() ,
,
∴A(4,0),AD=-m,
∵M、N分别为CD、OA的中点,
∴M(![]() ,
,![]() ),N(2,0),
),N(2,0),
∴MN=![]() ,
,
∴![]() ;
;
(3)如图3,延长GE交x轴于点J,则GJ⊥x轴,过点F作FK⊥GJ于点K,
∵E、F两点在射线OP上移动且P(2,2),
∴OP所以直线解析式为:y=x,
∴∠EOJ=∠EFK =45°,
∵EF=![]() ,
,
∴EK=FK=EG=2,
∵E(t,t),
∴G(t,t+2),F(t-2,t-2),
设直线HE解析式为:y=kx+b(k≠0),
将点E(t,t),H(-2t,0)代入可得:![]() ,
,
解得: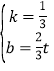 ,
,
∴直线HE解析式为:y=![]() x+
x+![]() ,
,
设直线FG解析式为:y=k1x+b1(k≠0),
将点 G(t,t+2),F(t-2,t-2)代入可得:![]() ,
,
解得:![]() ,
,
∴直线FG解析式为:y=2x+2-t,
联立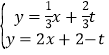 ,解得:
,解得: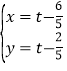 ,
,
即Q(![]() ,
,![]() ),
),
∵![]() ,
,
∴点Q在直线![]() 上运动.
上运动.

【题目】将图1中的正方形剪开得到图2,则图2中共有4个正方形;将图2中的一个正方形剪开得到图3,则图3中共有7个正方形;……如此剪下去,则第n个图形中正方形的个数是多少?

(1)将下表填写完整:
图(n) | 1 | 2 | 3 | 4 | 5 | …… | n |
正方形的个数 | 1 | 4 | 7 | …… | an |
(2)an= (用含n的代数式表示)
(3)按照上述方法,能否得到2019个正方形?如果能,请求出n;如果不能,请简述理由.