题目内容
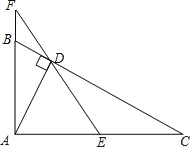
【题目】如图所示,将两条宽度相同的纸条交叉重叠放在一起,则重叠部分ABCD是________形,若纸条宽DE=4 cm,CE=3 cm,则四边形ABCD的面积为________.
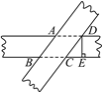
【答案】菱 20cm2
【解析】
过点A作AH⊥BC于点H,AF⊥CD于点F,首先可判断重叠部分为平行四边形,且两条纸条宽度相同,证Rt△ABH≌Rt△DAF,可知AB=AD,即可ABCD是菱形;由勾股定理可得CD=5,再由菱形面积计算方法可得面积.
如图,过点A作AH⊥BC于点H,DF⊥CD于点F,
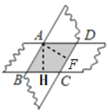
则AH=AF,
由题意得:AB∥CD,BC∥AD,
∴四边形ABCD是平行四边形,
∴∠ABC=∠CDA,
在Rt△ABH和Rt△DAF中,
∵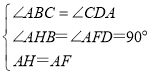 ,
,
∴Rt△ABH≌Rt△DAF,
∴AB=AD,
∴平行四边形ABCD是菱形.
在Rt△CDE中,DE=4 cm,CE=3 cm,∠DEC=90°,
∴CD=![]()
∴菱形ABCD的面积=5×4=20cm2.
故答案为:菱;20cm2.

练习册系列答案
 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案
相关题目
【题目】将图1中的正方形剪开得到图2,则图2中共有4个正方形;将图2中的一个正方形剪开得到图3,则图3中共有7个正方形;……如此剪下去,则第n个图形中正方形的个数是多少?

(1)将下表填写完整:
图(n) | 1 | 2 | 3 | 4 | 5 | …… | n |
正方形的个数 | 1 | 4 | 7 | …… | an |
(2)an= (用含n的代数式表示)
(3)按照上述方法,能否得到2019个正方形?如果能,请求出n;如果不能,请简述理由.