题目内容
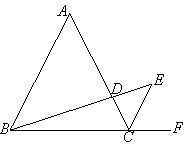
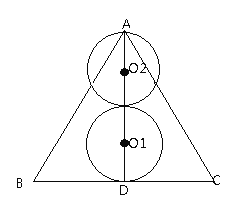
【题目】已知等边△ABC边长为2，D为BC中点,连接AD.点O在线段AD上运动（不含端点A、D），以点O为圆心，
长为半径作圆，当
O与△ABC的边有且只有两个公共点时，DO的取值范围为_____.
【答案】
或
【解析】
根据题意作图，根据
O与△ABC的边有且只有两个公共点时得到两种情况，分别讨论求解即可.
∵O与△ABC的边有且只有两个公共点
∴①当圆O与BC相交于两点时，
如图，点圆O1与BC相切时，恰好有一个交点，此时，O1D=
，
故当时，O与△ABC的边有且只有两个公共点；
②当圆O与△ABC的AB、AC各交于一点时，
∵等边△ABC边长为2，D为BC中点
∴∠B=∠BAC=60°，AD为△ABC的高、中线、∠BAC的角平分线，
∴BD=1，则AD=
如图，圆O2与△交于3点，此时AO2=,
则O2D=
-=
∵O与△ABC的边有且只有两个公共点，则点A在圆O内部，
∴当时，O与△ABC的边有且只有两个公共点；
综上，当或时，O与△ABC的边有且只有两个公共点.
故填：或.
练习册系列答案
黄冈冠军课课练系列答案
相关题目
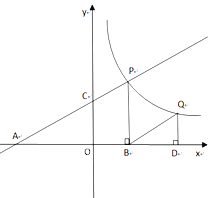
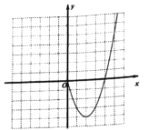
【题目】某课外学习小组根据学习函数的经验，对函数
的图象与性质进行了探究请补充完整以下探索过程：
（1）列表：
x | … | -5 | -4 | -3 | -2 | -1 | 0 | 1 | 2 | 3 | 4 | … |
y | … | m | 0 | -3 | -4 | -3 | 0 | -3 | -4 | n | 0 | … |
直接写出
________，
________；
（2）根据上表中的数据，在平面直角坐标系内补全该函数的图象，并结合图象写出该函数的两条性质：
性质1______________________________________________________
性质2_______________________________________________________
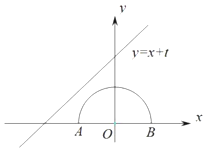
（3）若方程
有四个不同的实数根，请根据函数图象，直接写出k的取值范围.
