题目内容
【题目】如图,在矩形ABCD中,AB=8,AD=6,将矩形ABCD绕点A逆时针旋转得到矩形AEFG.
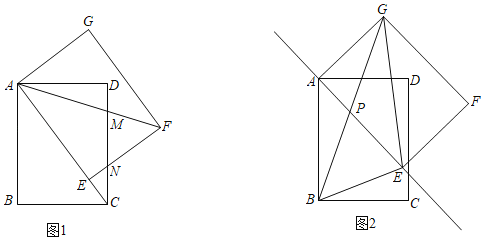
(1)如图1,若在旋转过程中,点E落在对角线AC上,AF,EF分别交DC于点M,N.
①求证:MA=MC;
②求MN的长;
(2)如图2,在旋转过程中,若直线AE经过线段BG的中点P,连接BE,GE,求△BEG的面积
【答案】(1)①见解析;②![]() ;(2)△BEG的面积为48﹣6
;(2)△BEG的面积为48﹣6![]() 或48+6
或48+6![]()
【解析】
(1)①由矩形的性质得出![]() ,得出
,得出![]() ,由旋转的性质得:
,由旋转的性质得:![]() ,证出
,证出![]() ,即可得出
,即可得出![]() ;
;
②设![]() ,则
,则![]() ,在
,在![]() 中,由勾股定理得出方程
中,由勾股定理得出方程![]() ,解得:
,解得:![]() ,在
,在![]() 中,由勾股定理得出
中,由勾股定理得出![]() ,得出
,得出![]() ,证出
,证出![]() ,得出
,得出![]() 即可;
即可;
(2)分情况讨论:①过点![]() 作
作![]() 于
于![]() ,证明
,证明![]() ,得出
,得出![]() ,
,![]() ,在
,在![]() 中,由勾股定理得出
中,由勾股定理得出![]() ,得出
,得出![]() ,得出
,得出![]() ,得出
,得出![]() 的面积
的面积![]() 的面积
的面积![]() ;
;
②同①得:![]() ,
,![]() ,得出
,得出![]() ,得出
,得出![]() 的面积
的面积![]() 的面积
的面积![]() 即可.
即可.
(1)①证明:![]() 四边形
四边形![]() 是矩形,
是矩形,
![]() ,
,
![]() ,
,
由旋转的性质得:![]() ,
,
![]() ,
,
![]() ;
;
②解:设![]() ,则
,则![]() ,
,
在![]() 中,
中,![]() ,
,
解得:![]() ,
,
在![]() 中,
中,![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
又![]() ,
,
![]() ,
,
![]() ;
;
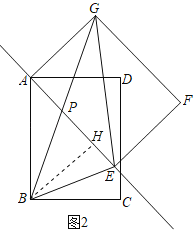
(2)解:分情况讨论:
①如图2所示:过点![]() 作
作![]() 于
于![]() ,则
,则![]() ,
,
在![]() 和
和![]() 中,
中,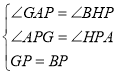 ,
,
![]() ,
,
![]() ,
,![]() ,
,
在![]() 中,
中,![]() ,
,
![]() ,
,
![]() ,
,
![]() 的面积
的面积![]() 的面积
的面积![]() ;
;
②如图3所示:
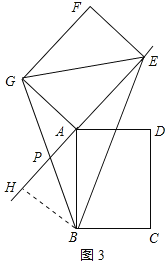
同①得:![]() ,
,![]() ,
,
![]() ,
,
![]() 的面积
的面积![]() 的面积
的面积![]() ;
;
综上所述,![]() 的面积为
的面积为![]() 或
或![]() .
.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目