Question

【题目】如图1，与都是等腰直角三角形，直角边，在同一条直线上，点、分别是斜边、的中点，点为的中点，连接，，，，．

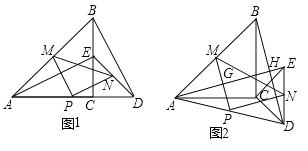
（1）观察猜想：

图1中，与的数量关系是______，位置关系是______．

（2）探究证明：

将图1中的绕着点顺时针旋转，得到图2，与、分别交于点、，判断的形状，并说明理由；

（3）拓展延伸：

把绕点任意旋转，若，，请直接写出面积的最大值．

Answer 1

【答案】（1），；（2）的形状为等腰直角三角形，理由见解析；（3）的面积的最大值为．

【解析】

（1）延长AE交BD于点H，易证ΔACE≌ΔBCD，得AE=BD，∠CAE=∠CBD，进而得∠BHA=90°，结合中位线的性质，得PM=BD，PM//BD，PN=AE， PN//AE，进而得PM=PN，PM⊥PN；

（2）设AE交BC于⊙O，易证ΔACE≌ΔBCD，得AE=BD，∠CAE=∠CBD，进而得∠BHA=90°，结合中位线的性质，得PM=BD，PM//BD，PN=AE， PN//AE，进而得PM=PN，PM⊥PN；

（3）易证ΔPMN是等腰直角三角形，PM=BD，当B、C、D共线时，BD的值最大，进而求解．

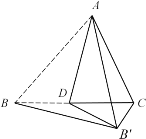
解：（1）如图1，

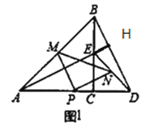
延长AE交BD于点H，

∵ΔACB和ΔECD是等腰直角三角形，

∴AC=BC，EC=CD，

∠ACB=∠ECD=90°，

∴∠ACB+∠BCE=∠ECD+∠BCE，

∴∠ACE=∠BCD，

∴ΔACE≌ΔBCD（SAS），

∴AE=BD，∠CAE=∠CBD，

又∵∠AEC=∠BEH，

∴∠BHA=∠ACE=90°，

∵点P、M、N分别为AD、AB、DE的中点，

∴PM=BD，PM//BD，PN=AE，PN//AE，

∴PM=PN，

∴PM⊥AH，

∴PM⊥PN．

（2）如图中，设交于．

∵和是等腰直角三角形，

∴，，

∴

∴.∴

∴，

又∵，，∴

∵点、、分别为、、的中点，∴，；

，.∴

∴

∴

∴

∴

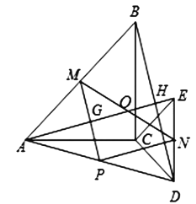
（3）的面积的最大值为．

由（2）可知是等腰直角三角形，，

∴当的值最大时，的值最大，的面积最大，

∴当、、共线时，的最大值，∴，

∴的面积的最大值．