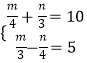题目内容
【题目】已知一元二次方程x2﹣2x+m﹣1=0.
(1)当m取何值时,方程有两个不相等的实数根?
(2)设x1,x2是方程的两个实数根,且满足x12+x1x2=1,求m的值.
【答案】(1)m<2;(2)m=![]() .
.
【解析】
试题分析:(1)若一元二次方程有两不等实数根,则根的判别式△=b2﹣4ac>0,建立关于m的不等式,即可求出m的取值范围.(2)x1是方程的实数根,就适合原方程,可得到关于x1与m的等式.再根据根与系数的关系知,x1x2=m﹣1,故可求得x1和m的值.
试题解析:(1)根据题意得△=b2﹣4ac=4﹣4×(m﹣1)>0,解得m<2;(2)∵x1是方程的实数根,∴x12﹣2x1+m﹣1=0 ①,∵x1,x2是方程的两个实数根,∴x1x2=m﹣1,∵x12+x1x2=1,∴x12+m﹣1=1 ②,由①②得x1=0.5,把x=0.5代入原方程得,m=![]() .
.

练习册系列答案
 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案
相关题目