Question

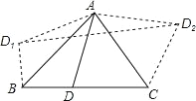
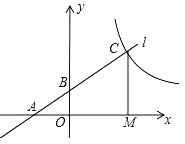
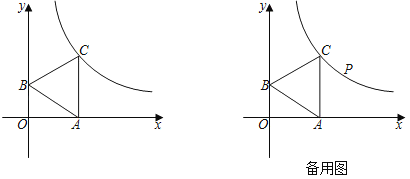
【题目】如图，点A、B分别在x轴和y轴的正半轴上，以线段AB为边在第一象限作等边△ABC，，且CA∥y轴．

（1）若点C在反比例函数的图象上，求该反比例函数的解析式；

（2）在（1）中的反比例函数图象上是否存在点N，使四边形ABCN是菱形，若存在请求出点N坐标，若不存在，请说明理由．

（3）点P在第一象限的反比例函数图象上，当四边形OAPB的面积最小时，求出P点坐标．

Answer 1

【答案】（1）y＝；（2）存在，N（2，1）；（3）P（，）．

【解析】

（1）如图1中，作CD⊥y轴于D．首先证明四边形OACD是矩形，利用反比例函数k的几何意义解决问题即可．

（2）如图2中，作BD⊥AC于D，交反比例函数图象于N，连接CN，AN．求出的坐标，证明四边形ABCN是菱形即可．

（3）如图3中，连接PB，PA，OP．设P（a，）．可得S四边形OAPB＝S△POB+S△POA＝ ×1×a+××＝a+＝由此即可解决问题．

解：（1）如图1中，作CD⊥y轴于D．

∵CA∥y轴，CD⊥y轴，

∴CD∥OA，AC∥OD，

∴四边形OACD是平行四边形，

∵∠AOD＝90°，

∴四边形OACD是矩形，

∴k＝S矩形OACD＝2S△ABC＝，

∴反比例函数的解析式为y＝．

（2）如图2中，作BD⊥AC于D，交反比例函数图象于N，连接CN，AN．

∵△ABC是等边三角形，面积为，设CD＝AD＝m，则BD＝m，

∴×2m×m＝，

∴m＝1或﹣1（舍弃），

∴B（0，1），C（，2），A（，0），

∴N（2，1），

∴BD＝DN，

∵AC⊥BN，

∴CB＝CN，AB＝AN，

∵AB＝BC，

∴AB＝BC＝CN＝AN，

∴四边形ABCN是菱形，

∴N（2，1）．

（3）如图3中，连接PB，PA，OP．设P（a，）．

S四边形OAPB＝S△POB+S△POA＝×1×a+××＝a+＝

∴当a＝时，四边形OAPB的面积最小，

解得a＝或（舍弃），

此时P（，）．