题目内容
如图，在□ABCD中，点E，F分别是BC和AD上的两点，且AE∥CF，延长AE与DC延长线交于点G，延长CF与BA的延长线交于点H，求证：HF = GE．
见解析
证明：∵四边形ABCD是平行四边形
∴AB∥CD， AD∥BC
∴AF∥CE, AH∥CG
∵AE∥CF且AF∥CE
∴四边形AECF是平行四边形
∴AE =" CF··············" 5分
∵AG∥CH且AH∥CG
∴四边形AGCH是平行四边形
∴AG =" CH··································" 10分
∴AG
AE = CHCF
∴GE = HF 12分
首先利用定义证明四边形AECF为平行四边形，进而得出AE = CF，从而可得出四边形AGCH是平行四边形，进而得出AG = CH，最后得出结论
∴AB∥CD， AD∥BC
∴AF∥CE, AH∥CG
∵AE∥CF且AF∥CE
∴四边形AECF是平行四边形
∴AE =" CF··············" 5分
∵AG∥CH且AH∥CG
∴四边形AGCH是平行四边形
∴AG =" CH··································" 10分
∴AG
AE = CHCF∴GE = HF 12分
首先利用定义证明四边形AECF为平行四边形，进而得出AE = CF，从而可得出四边形AGCH是平行四边形，进而得出AG = CH，最后得出结论
练习册系列答案
相关题目
ABCD，E是BA延长线上一点，AB=AE，连接CE交AD于点F，若CF平分∠BCD，AB=3，则BC的长为 ．
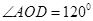，AB=2.5，则AC的长为 。
