ΧβΡΩΡΎ»ί
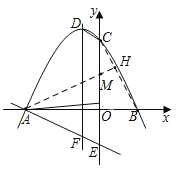
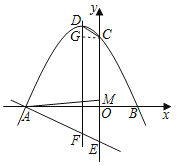
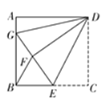
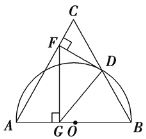
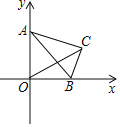
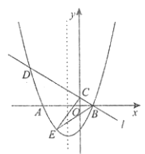
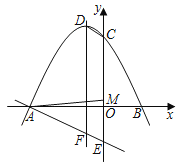
ΓΨΧβΡΩΓΩ»γΆΦΘ§Εΰ¥ΈΚ· ΐyΘΫax2+2ax+cΘ®aΘΦ0Θ©ΒΡΆΦœσ”κx÷αΫΜ”ΎAΓΔBΝΫΒψΘ§”κy÷αΫΜ”ΎCΒψΘ§ΕΞΒψΈΣDΘ§“Μ¥ΈΚ· ΐyΘΫmx©¹3ΒΡΆΦœσ”κy÷αΫΜ”ΎEΒψΘ§”κΕΰ¥ΈΚ· ΐΒΡΕ‘≥Τ÷αΫΜ”ΎFΒψΘ§«“tanΓœFDCΘΫ![]() Θ°
Θ°
Θ®1Θ©«σaΒΡ÷ΒΘΜ
Θ®2Θ©»τΥΡ±Ώ–ΈDCEFΈΣΤΫ––ΥΡ±Ώ–ΈΘ§«σΕΰ¥ΈΚ· ΐ±μ¥ο ΫΘ°
Θ®3Θ©‘ΎΘ®2Θ©ΒΡΧθΦΰœ¬…ηΒψM «œΏΕΈOC…œ“ΜΒψΘ§Ν§Ϋ”AMΘ§ΒψP¥”ΒψA≥ωΖΔΘ§œ»“‘1ΗωΒΞΈΜ≥ΛΕ»/sΒΡΥΌΕ»―ΊœΏΕΈAMΒΫ¥οΒψMΘ§‘Ό“‘![]() ΗωΒΞΈΜ≥ΛΕ»/sΒΡΥΌΕ»―ΊMCΒΫ¥οΒψCΘ§«σΒψPΒΫ¥οΒψCΥυ”ΟΉνΕΧ ±ΦδΈΣΓΓ sΘ®÷±Ϋ”–¥≥ω¥πΑΗΘ©Θ°
ΗωΒΞΈΜ≥ΛΕ»/sΒΡΥΌΕ»―ΊMCΒΫ¥οΒψCΘ§«σΒψPΒΫ¥οΒψCΥυ”ΟΉνΕΧ ±ΦδΈΣΓΓ sΘ®÷±Ϋ”–¥≥ω¥πΑΗΘ©Θ°
ΓΨ¥πΑΗΓΩΘ®1Θ©aΘΫ©¹![]() ΘΜΘ®2Θ©yΘΫ©¹
ΘΜΘ®2Θ©yΘΫ©¹![]() x2©¹
x2©¹![]() x+6ΘΜΘ®3Θ©
x+6ΘΜΘ®3Θ©![]() Θ°
Θ°
ΓΨΫβΈωΓΩ
Θ®1Θ©ΙΐΒψCΉςCGΓΆDFΫΜ”ΎΒψGΘ§«σ≥ωC”κDΒψΉχ±ξΘ§Ω…ΒΟCG=1Θ§DG=-aΘ§‘Ό”…tanΓœFDC=![]() Θ§Φ¥Ω…«σaΒΡ÷ΒΘΜ
Θ§Φ¥Ω…«σaΒΡ÷ΒΘΜ
Θ®2Θ©”…ΒψΒΡΉχ±ξΖ÷±π«σ≥ωCE=3+cΘ§DF=c+![]() +m+3Θ§‘Ό”…ΤΫ––ΥΡ±Ώ–ΈΒΡ–‘÷ Ω…ΒΟ3+c=c+
+m+3Θ§‘Ό”…ΤΫ––ΥΡ±Ώ–ΈΒΡ–‘÷ Ω…ΒΟ3+c=c+![]() +m+3Θ§Ω…“‘»ΖΕ®y=-
+m+3Θ§Ω…“‘»ΖΕ®y=-![]() x-3Θ§«σ≥ωAΒψΉχ±ξΘ§ΫΪAΒψΉχ±ξ¥ζ»κy=-
x-3Θ§«σ≥ωAΒψΉχ±ξΘ§ΫΪAΒψΉχ±ξ¥ζ»κy=-![]() x2-
x2-![]() x+cΘ§Φ¥Ω…«σ≥ωcΒΡ÷ΒΘΜ
x+cΘ§Φ¥Ω…«σ≥ωcΒΡ÷ΒΘΜ
Θ®3Θ©Ν§Ϋ”BCΘ§ΙΐΒψAΉςAHΓΆBCΫΜ”ΎΒψHΘ§AH”κCOΒΡΫΜΒψΈΣΥυ«σMΘΜ”…Χβ“βΩ…÷Σ‘ΥΕ· ±ΦδΈΣAM+![]() ΘΜ‘ΎRtΓςCMH÷–Θ§MH=CMsinΓœBCO=
ΘΜ‘ΎRtΓςCMH÷–Θ§MH=CMsinΓœBCO=![]() Θ§‘ρ”–AM+
Θ§‘ρ”–AM+![]() =AM+MH=AHΘΜ‘Ό‘ΎRtΓςABH÷–Θ§AB=6Θ§sinΓœCOB=ΘΫ
=AM+MH=AHΘΜ‘Ό‘ΎRtΓςABH÷–Θ§AB=6Θ§sinΓœCOB=ΘΫ![]() ΘΫ
ΘΫ![]() Θ§
Θ§
«σ≥ωAH=ABsinΓœCOB=6ΓΝ![]() ΘΫ
ΘΫ![]() Θ§Φ¥ΈΣΥυ«σΘ°
Θ§Φ¥ΈΣΥυ«σΘ°
Θ®1Θ©ΙΐΒψCΉςCGΓΆDFΫΜ”ΎΒψGΘ§
ΓΏCΘ®0Θ§cΘ©Θ§DΘ®©¹1Θ§c©¹aΘ©Θ§
ΓύCGΘΫ1Θ§DGΘΫ©¹aΘ§
ΓΏtanΓœFDCΘΫ![]() Θ§
Θ§
Γύ![]() ΘΫ
ΘΫ![]() Θ§
Θ§
ΓύaΘΫ©¹![]() ΘΜ
ΘΜ
Θ®2Θ©ΓΏaΘΫ©¹![]() Θ§
Θ§
ΓύDΘ®©¹1Θ§c+![]() Θ©Θ§
Θ©Θ§
ΓΏEΘ®0Θ§©¹3Θ©Θ§FΘ®©¹1Θ§©¹m©¹3Θ©Θ§
ΓύCEΘΫ3+cΘ§DFΘΫc+![]() +m+3Θ§
+m+3Θ§
ΓΏΥΡ±Ώ–ΈDCEFΈΣΤΫ––ΥΡ±Ώ–ΈΘ§
Γύ3+cΘΫc+![]() +m+3Θ§
+m+3Θ§
ΓύmΘΫ©¹![]() Θ§
Θ§
ΓύyΘΫ©¹![]() x©¹3Θ§
x©¹3Θ§
ΓύAΘ®©¹4Θ§0Θ©Θ§
ΫΪAΘ®©¹4Θ§0Θ©¥ζ»κyΘΫ©¹![]() x2©¹
x2©¹![]() x+cΘ§
x+cȧ
Ω…ΒΟcΘΫ6Θ§
ΓύyΘΫ©¹![]() x2©¹
x2©¹![]() x+6ΘΜ
x+6ΘΜ
Θ®3Θ©Ν§Ϋ”BCΘ§ΙΐΒψAΉςAHΓΆBCΫΜ”ΎΒψHΘ§AH”κCOΒΡΫΜΒψΈΣΥυ«σMΘΜ
”…Χβ“βΩ…÷Σ‘ΥΕ· ±ΦδΈΣAM+![]() ΘΜ
ΘΜ
ΓΏyΘΫ©¹![]() x2©¹
x2©¹![]() x+6Θ§Ω…«σBΘ®2Θ§0Θ©Θ§
x+6Θ§Ω…«σBΘ®2Θ§0Θ©Θ§
‘ΎRtΓςBCO÷–Θ§OBΘΫ2Θ§OCΘΫ6Θ§
ΓύBCΘΫ2![]() Θ§
Θ§
ΓύsinΓœBCOΘΫ![]() ΘΫ
ΘΫ![]() Θ§
Θ§
‘ΎRtΓςCMH÷–Θ§MHΘΫCMsinΓœBCOΘΫ![]() Θ§
Θ§
ΓύAM+![]() ΘΫAM+MHΘΫAHΘΜ
ΘΫAM+MHΘΫAHΘΜ
‘ΎRtΓςABH÷–Θ§ABΘΫ6Θ§sinΓœCOBΘΫ![]() ΘΫ
ΘΫ![]() Θ§
Θ§
ΓύAHΘΫABsinΓœCOBΘΫ6ΓΝ![]() ΘΫ
ΘΫ![]() Θ§
Θ§
ΓύΒψPΒΫ¥οΒψCΥυ”ΟΉνΕΧ ±ΦδΈΣ![]() sΘ§
sȧ
Ι ¥πΑΗΈΣ![]() ΘΜ
ΘΜ