Question

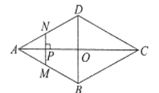
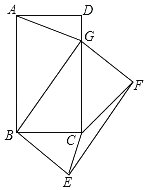
【题目】如图，在矩形ABCD中，AB＝5，BC＝3，将矩形ABCD绕点B按顺时针方向旋转得到矩形GBEF，点A落在矩形ABCD的边CD上，连结CE，CF，若∠CEF＝α，则tanα＝_____．

Answer 1

【答案】．

【解析】

过C点作MN⊥BG，交BG于M，交EF于N，由旋转的性质可得∠ABC=∠GBE=90°，BA=BG=5，BC=BE=3，由勾股定理可求CG=4，由锐角三角函数可求CM的长，即可求BM的长，由题意可证四边形BENM是矩形，可求EN，CN的长，即可求解．

过C点作MN⊥BG，交BG于M，交EF于N，

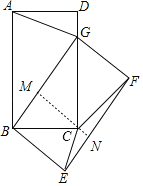
由旋转变换的性质可知，∠ABC＝∠GBE＝90°，BA＝BG＝5，BC＝BE＝3，

由勾股定理得，CG＝＝＝4，

∵sin∠GBC＝，

∴

∴CM＝，

∴BM＝＝

∵MN⊥BG，∠GBE＝∠BEF＝90°，

∴四边形BENM是矩形，

∴MN＝BE＝3，BM＝EN＝，

∴CN＝3﹣＝，

∴tanα＝＝＝

故答案为：．