题目内容
【题目】如图,等腰△ABC和等腰△ADE的顶角∠BAC=∠DAE=30°,△ACE可以看作是△ABD经过什么图形变换得到的?说明理由.
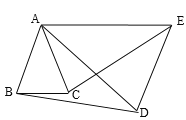
【答案】以A点为中心逆时针旋转30°得到的,其理由见解析
【解析】
△ACE的两边AC、AE分别是等腰△ABC和等腰△ADE的两腰,由此联想到它们的另外两腰,AB、AD,公共顶点都是点A,且∠BAC=∠DAE=30°,故可得答案.
△ACE可以看作是△ABD以A点为中心逆时针旋转30°得到的,其理由如下:
∵∠BAC=∠DAE,
∴∠BAD=∠CAE,
又∵AB=AC,AD=AE,
∴△ABD≌△ACE(SAS)
又∵∠BAC=∠DAE=30°,
∴△ACE可以看作是△ABD以A点为中心逆时针旋转30°得到的.

练习册系列答案
相关题目